Advertisements
Advertisements
Question
|
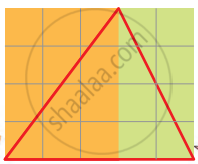
Sameena Both the big triangles in this rectangle have the same area. |
 |
Sadiq But these look very different. |
|
The blue triangle is half of the big rectangle. The area of the big rectangle is 20 square cm. So the area of the blue triangle is ______ square cm. |
And what about the red triangle? |
|
|
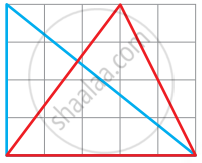
Ah, in it there are two halves of two different rectangles! |
|
Now you find the area of the two rectangles Sadiq is talking about. What is the area of the red triangle? Explain. |
|
Yes, you are right. And you know what!! You can draw many more triangles of the area of 10 square cm in this rectangle. Try drawing them. |
Help Sadiq in finding some more such triangles. Draw at least 5 more. |
Solution
- The blue triangle is half of the big rectangle. The area of the big rectangle is 20 square cm. So the area of the blue triangle is 10 square cm.
Explanation:
Area of the blue triangle
= `1/2 xx 20`
= 10 square cm - The area of the red triangle is half of the area of the rectangle. Hence, the area of the red triangle = is 10 square cm.
- Area of two rectangles = Area of red rectangle + area of green rectangle
= (3 × 4) + (4 × 2)
= 12 + 8 = 20 square cm Hence, area of red triangle together
= Half of the area of both rectangles together
= `1/2 xx 20` = 10 square cm.
Hence, both triangles have the same area. 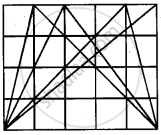
Four triangles having an area of 10 cm2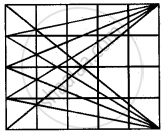
Five triangles having an area of 10 cm2
APPEARS IN
RELATED QUESTIONS
Make big squares and rectangles like this to find the area faster.

What is the area of this triangle?

The triangle is half the rectangle of an area of 2 square cm. So its area is ______ square cm.
The triangle is half the rectangle of an area of 2 square cm. So its area is ____________ square cm.
And what about the red triangle?

Now you find the area of the two rectangles Sadiq is talking about. What is the area of the red triangle? Explain
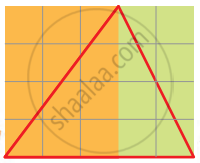
 |
Oh, I thought of doing it differently! If you draw like this, the area is still 10 square cm. |
Is Suruchi correct? How much is the blue area? Explain
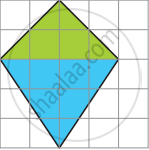
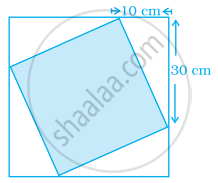
Here is a rectangle of an area of 20 square cm.

Draw one straight line in this rectangle to divide it into two equal triangles. What is the area of each of the triangles?
Here is a rectangle of an area of 20 square cm.

Draw two straight lines in this rectangle to divide it into one rectangle and two equal triangles.
What is the area of the rectangle?
What is the area of each of the triangles?
A design is made up of four congruent right triangles as shown in the given figure. Find the area of the shaded portion.