Advertisements
Advertisements
Question
Show that a. (b × c) is equal in magnitude to the volume of the parallelepiped formed on the three vectors, a, b and c.
Solution
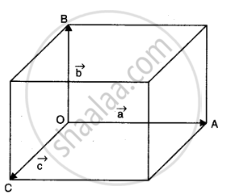
Let a parallelopiped be formed on the three vectors.
`vec(OA) = veca`, `vec(OB) = vecb` and `vec(OC) = vecC`
Now `vecb xx vecc = bc sin 90^@ hatn`
`= bc hatn`
where `hatn` is unit vector along `vec(OA)` perpendicular to the plane containing `vecb` and `vecc`
Now `veca.(vecb xx vecc) = veca.bc hatn`
`=(a)(bc) cos 0^@`
= abc
which is equal in magnitude to the volume of the parallelopiped.
APPEARS IN
RELATED QUESTIONS
Let \[\overrightarrow A\] be a unit vector along the axis of rotation of a purely rotating body and \[\overrightarrow B\] be a unit vector along the velocity of a particle P of the body away from the axis. The value of \[\overrightarrow A.\overrightarrow B\] is ____________ .
Let \[\overrightarrow F\] be a force acting on a particle having position vector \[\overrightarrow r.\] Let \[\overrightarrow\Gamma\] be the torque of this force about the origin, then __________ .
Show that the area of the triangle contained between the vectors a and b is one half of the magnitude of a × b.
