Advertisements
Advertisements
Question
Six equal resistors of 1 ohm each are connected to form the sides of a hexagon ABCDEF. Calculate the resistance offered by the combination if the current enters at A and leaves it at D.
Solution
From figure it is clear that there are two sets of parallel resistances between A and D. Each group has three resistances of 1Ω each, in series.
Equivalent resistance R1 of one group (AB, BC and CD) = 1Ω + 1Ω + 1Ω = 3Ω
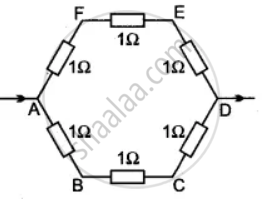
Similarly equivalent resistance R2 of the other group (AF, FE, ED)
= 1Ω + 1Ω + 1Ω = 3Ω
As the two groups are in parallel, we have
`1/"R" = 1/"R"_1 + 1/"R"_2 = 1/3 + 1/3 = 2/3`
where R is the equivalent resistance of the whole combonation.
∴ R = `3/2` Ω or 1.5 Ω.
APPEARS IN
RELATED QUESTIONS
In series combination which remains constant?
(a) Voltage
(b) Current
(c) Both current and voltage
(d) Both are variables
Why is the series arrangement not used for domestic circuits?
Name the material which is used for making the heating element of an electric iron.
What possible values of resultant resistance one can get by combining two resistances, one of value 2 ohm and the other 6 ohm?
How does the resistivity of a semiconductor depend on temperature?
The voltage applied to a given rheostat is made four times its initial value. By what factor will be resistance of the rheostat change?
You are provided with three resistors of resistance 1.0 Ω, 2.0 Ω and 3.0 Ω How would you connect them to obtain the total effective resistance 1.5 Ω? Draw diagram of the arrangement and check it by calculations.
What is the equivalent resistance between the points X and Y for the given network?
Two electric bulbs have resistances in the ratio 1 : 2. If they are joined in series, the energy consumed in them is in the ratio:
