Question

Sketch the graphs of the following functions:

y = `(x^2 + 1)/(x^2 - 4)`

Answer 1

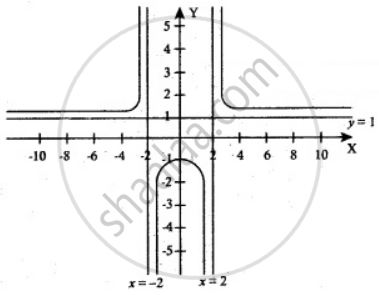
The domain of the given function f(x) is `(-oo, -2) ∪ (-2, 2) ∪ (2, oo)`

ie. x < – 2 or – 2 < x < 2 or x > 2.

Range of f(x) is `(- oo, - 1/4) ∪ (1, oo)`

i.,e. `"f"(x) ≤ - 1/4` or f(x) > 1

Putting y = 0, x is unreal.

Hence, there is no ‘x’ intercept.

By putting x = 0, we get y = `- 1/4`

∴ y intercept is  `(0, - 1/4)`

f'(x) = `- (10x)/(x^2 - 4)^2`

f'(x) = 0

⇒ x = 0

∴ The critical point is at x = 0

f'(x) = `(10(x^2 - 4)(3x + 4))/((x^2 - 4)^4`

f'(0) = `- 5/8 < 0`

∴ f(x) is maximum at x = 0.

Hence the local maximum is f(0) = `- 1/4`

No points of inflection exist for the curve.

When x = ± 2, y = `oo`

∴ Vertical asymptotes are x = 2 and x = – 2 and Horizontal asymptote is y = 1.