Advertisements
Advertisements
Question
संलग्न आकृति में A केंद्र वाले वृत्त में ∠PAR = 30° AP = 7.5 हो तो, वृत्तखंड PQR का क्षेत्रफल ज्ञात कीजिए। (π = 3.14)
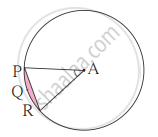
Solution
वृत्त की त्रिज्या (r) = AP = 7.5
m(चाप PQR) = ∠PAR = θ = 30°
वृत्तखंड PQR का क्षेत्रफल = `r^2[(pitheta)/360 - sintheta/2]`
= `7.5^2[(3.14 xx 30)/360 - sin 30/2]`
= `7.5^2[3.14/12 - 1/(2 xx 2)]` ................[sin 30 = `1/2`]
= `7.5^2[3.14/12 - 1/4]`
= `7.5^2[(3.14 - (1 xx 3))/12]`
= `7.5^2 xx [(3.14 - 3)/2]`
= `56.25 xx 0.14/12`
= `7.875/12`
= 0.65625 वर्ग इकाई |
वृत्तखंड PQR का क्षेत्रफल 0.65625 वर्ग इकाई है |
APPEARS IN
RELATED QUESTIONS
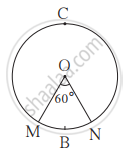
संलग्न आकृति में वृत्त की त्रिज्या 7 सेमी है और m(चाप MBN) = 60° तो
(1) वृत्त का क्षेत्रफल ज्ञात कीजिए।
(2) A(O - MBN) ज्ञात कीजिए।
(3) A(O - MCN) ज्ञात कीजिए।
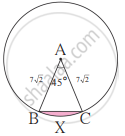
आकृति में बिंदु A केंद्रवाले वृत्त में ∠ABC = 45°, AC = `7sqrt2` सेमी, हो तो वृत्तखंड BXC का क्षेत्रफल ज्ञात कीजिए। (π = 3.14, `sqrt2` = 1.41)
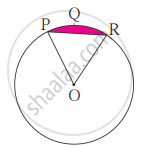
आकृति में बिंदु O वृत्त का केंद्र है। m(चाप PQR) = 60°, OP = 10 सेमी, हो तो छायांकित भाग का क्षेत्रफल ज्ञात कीजिए। (π = 3.14, `sqrt3` = 1.73)
आकृति में O केंद्रवाले किसी वृत्त में PQ जीवा है। ∠POQ = 90°, और छायांकित भाग का क्षेत्रफल 114 वसेमी हो तो वृत्त कि त्रिज्या ज्ञात कीजिए। (π = 3.14)
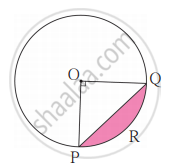
15 सेमी त्रिज्यावाले किसी वृत्त में जीवा PQ वृत्त के केंद्र से 60° का कोण बनाती है। उस जीवा से बनने वाले दीर्घ वृत्तखंड और लघु वृत्तखंड का क्षेत्रफल ज्ञात कीजिए। (π = 3.14, `sqrt3` = 1.73)
