Advertisements
Advertisements
Question
Solve the following inequalities and represent the solution set on a number line:
-4 ≤ 2x - 3 ≤ 5
Solution
The given inequality -4 ≤ 2x - 3 ≤ 5 is equivalent to
3 - 4 ≤ 2x ≤ 5 + 3
⇒ -1 ≤ 2x ≤ 8
⇒ `-(1)/(2) ≤ x ≤ 4`
The graph of this set is -1/2 ≤ x ≤ 4.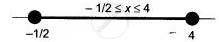
APPEARS IN
RELATED QUESTIONS
Solve the following inequation, write down the solution set and represent it on the real number line:
–2 + 10x ≤ 13x + 10 < 24 + 10x, x 𝜖 Z
Solve the following in equation and represent the solution set on the number line.
`R - 3 < -1/2 - (2x)/3 <= 5/6, x ∈ R`
Represent the following inequalities on real number line:
3x + 1 ≥ – 5
Represent the solution of the following inequalities on the real number line:
x + 3 ≤ 2x + 9
Represent the solution of the following inequalities on the real number line:
`(2x + 5)/3 > 3x - 3`
Use the real number line to find the range of values of x for which:
x > 3 and 0 < x < 6
Solve the following linear in-equation and graph the solution set on a real number line :
3x - 9 ≤ 4x - 7 < 2x + 5, x ∈ R
Solve the following inequation, write the solution set and represent it on the number line.
`-3 (x - 7) ≥ 15 - 7x > (x + 1)/3, x ∈ R`
Given:
P = {x : 5 < 2x - 1 ≤ 11, x ∈ R}
Q = {x : -1 ≤ 3 + 4x < 23, x ∈ R}
Where R = (real number), I = (Integers) Reperesnr P and Q on number lines. Write down the elements of P ∩ Q.
Solve the following inequation and represent the solution set on the number line : `-3 < -(1)/(2) - (2x)/(3) ≤ (5)/(6), x ∈ "R"`
