Advertisements
Advertisements
Question
State Gauss’s law in electrostatics. A cube which each side ‘a’ is kept is an electric field given by `vecE` = C × l. (as is shown in the figure where C is a positive dimensional constant. Find out
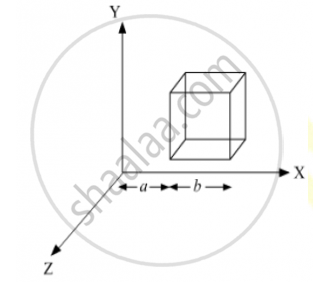
(i) The electric flux through the cube, and
(ii) The net charge inside the cube.
Solution
Gauss’ law states that the total electric flux through a closed surface that enclosed a charge is equal to
`1/in_0`times the magnitude of the charge enclosed.
Here, ∈0 is the absolute permittivity of the space
`phi=q/in_0`
q is the total charge enclosed
Also,`phi =oint_s vecE.vecds q/in_0`
Where `vecE`is the electric field at the area element`vecds.`
(ii) Now, the electric field `vecE=Cxhati` is in x-direction only. So faces with surface normal vector perpendicular to this field would give zero electric flux i.e. ∅ = Eds cos 90° = 0
So, flux would be across only two surfaces,
Magnitude of E at left face.
EL = Cx = Ca (x = a at left face)
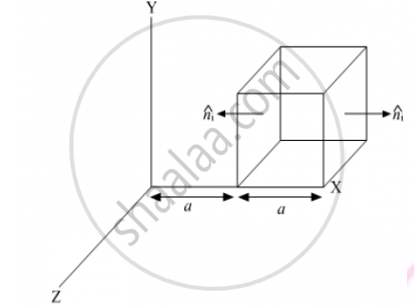
Magnitude of E at right face
ER = Cx = C2a = 2aC as (x = 2a at right face)
Thus, corresponding fluxes are
`phi_L = E_L *ds =E_L ds cos theta`
= `-a C xx a^2 (as theta = 180°)`
`phi^R = E_R *ds = 2a C ds costheta (theta =0)`
`=2aCa^2`
`=2a^3C`
Now, net flux through cube is
`=phi_L +phi_R`
`= -a^3 C+2a^3C`
`=a^3CNm^2C^-1`
(b) Net charge through cube
Again, we can use Gauss’s law to find total charge q inside the cube.
We have
`phi = q/in_0 or q =phi in_0`
`q =a^3Cin_0`Coulomb
RELATED QUESTIONS
In what way is Gauss's law in magnetism different from that used in electrostatics ? Explain briefly.
The susceptibility of magnesium at 300 K is 1.2 × 10−5. At what temperature will the susceptibility increase to 1.8 × 10−5?
According to Gauss’s law for magnetism ______.
Consider the two idealized systems: (i) a parallel plate capacitor with large plates and small separation and (ii) a long solenoid of length L >> R, radius of cross-section. In (i) E is ideally treated as a constant between plates and zero outside. In (ii) magnetic field is constant inside the solenoid and zero outside. These idealised assumptions, however, contradict fundamental laws as below:
Verify the Gauss’s law for magnetic field of a point dipole of dipole moment m at the origin for the surface which is a sphere of radius R.
A magnet is suspended horizontally in the earth's magnetic field. When it is displaced and then released it oscillates is a horizontal plane with a period T. If a piece of wood of same moment of inertia (about the axis of rotation) as the magnet is attached to the magnet, what would the new period of oscillation of the system become?
A short magnet produces a deflection of 30° when placed at certain distance in tanA position of magnetometer. If another short magnet of double the length and thrice the pole strength is placed at the same distance in tanB position of the magnetometer, the deflection produced will be:
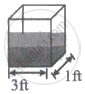
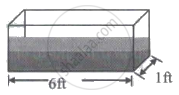
The figure shows two fish tanks, each having ends of width 1 foot. Tank A is 3 feet long while tank B is 6 feet long. Both tanks are filled with 1 foot of water.
SA = the magnitude of the force of the water on the end of tank A
SB = the magnitude of the force of the water on the end of tank B
BA = the magnitude of the force of the water on the bottom of tank A
BB = the magnitude of the force of the water on the bottom of tank B. Using the notation given above, Which one of the following sets of equations below is correct for this situation?
If the magnetic lines of force are shaped like arcs of concentric circles with their centre at point O in a certain section of a magnetic field ______.

