Advertisements
Advertisements
Question
State the theorem of parallel axes about moment of inertia.
Solution
Defination of moment of inertia :
A measure of the resistance of a body to angular acceleration about a given axis that is equal to the sum of the products of each element of mass in the body and the square of the element's distance from the axis.
Theorem of parallel axes:-
The moment of inertia of a body about any axis is equal to the sums of its moment of inertia about a parallel axis passing through its centre of mass and the product of its mass and the square of the perpendicular distance between the two parallel axes.
Mathematically , Io = Ic + Mh2
where Io = M. I of the body about any axis passing through centre O.
Ic = M. I of the body about parallel axis passing through centre of mass.
h = distance between two parallel axes.
Proof :
i) Consider a rigid body of mass M rotating about an axis passing through a point O as shown in the following
figure.
Let C be the centre of mass of the body, situated at distance h from the axis of rotation.
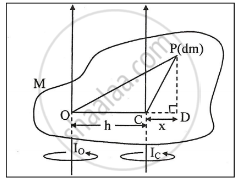
ii) Consider a small element of mass dm of the body, situated at a point P.
iii) Join PO and PC and draw PD perpendicular to OC when produced.
iv) M.I of the element dm about the axis through O is (OP)2 dm
∴ M.I of the body about the axis thorugh O is given by
Io = ∫ (OP)2 dm ......(1)
v) M.I of the element dm about the axis through c is CP2
dm
∴ M.I of the body about the axis through C
Ic = ∫ (CP)2 dm .....(2)
vi) From the figure,
OP2 = OD2 + PD2
= (OC + CD)2 + PD2
= OC2 + 2OC . CD + CD2 + PD2
∵ CP2 = CD2 + PD2
∴ OP2 = OC2 + 2 OC . CD + CP2 .....(3)
vii) From equation (1)
Io = ∫ (OP)2 dm
From equation (3)
`"I"_o = int ("OC"^2 + 2 "OC" . "CD" + "CP"^2) "dm"`
`therefore "I"_o = int ("h"^2 + 2"hx" + "CP"^2) "dm"`
`= int "h"^2 "dm" + int 2 "h.x" "dm" + int "CP"^2 "dm"`
`= "h"^2 int "dm" + 2"h" int "x" "dm" + int "CP"^2 "dm"`
`"I"_o = "h"^2 int "dm" + 2"h" int "x" "dm"`
[From equation (2)]
`therefore "I"_"o" = "I"_"c" + "h"^2 int "dm" + "2h" int "x dm"` .......(4)
viii) Since ∫ dm = M and ∫ x dm = 0 and
algebraic sum of the moments of the masses of its individual particles about the centre of mass is zero
for body in equilibrium.
∴ Equation (4) becomes
Io = Ic + Mh2
Hence proved.
RELATED QUESTIONS
A body of moment of inertia 5 kgm2 rotating with an angular velocity 6 rad/s has the same kinetic energy as a mass of 20 kg moving with a velocity of ......
A thin wire of length L and uniform linear mass density r is bent into a circular coil. M. I. of the coil about tangential axis in its plane is ................................
- `(3rhoL^2)/(8pi^2)`
- `(8pi^2)/(3rhoL^2)`
- `(3rhoL^3)/(8pi^2)`
- `(8pi^2)/(3rhoL^3)`
A body starts rotating from rest. Due to a couple of 20 Nm it completes 60 revolutions in one minute. Find the moment of inertia of the body.
A horizontal disc is freely rotating about a transverse axis passing through its centre at the rate of 100 revolutions per minute. A 20 gram blob of wax falls on the disc and sticks to the disc at a distance of 5 cm from its axis. Moment of intertia of the disc about its axis passing through its centre of mass is 2 x 10-4 kg m2. Calculate the new frequency of rotation of the disc.
The moment of inertia of a thin uniform rod of mass M and length L, about an axis passing through a point, midway between the centre and one end, perpendicular to its length is .....
(a)`48/7ML^2`
(b)`7/48ML^2`
(c)`1/48ML^2`
(d)`1/16ML^2`
A wheel of moment of inertia 1 Kgm 2 is rotating at a speed of 40 rad/s. Due to friction on the axis, the wheel comes to rest in 10 minutes. Calculate the angular momentum of the wheel, two minutes before it comes to rest.
A solid cylinder of uniform density of radius 2 cm has mass of 50 g. If its length is 12 cm, calculate its moment of inertia about an axis passing through its centre and perpendicular to its length.
Explain the physical significance of radius of gyration
A uniform solid sphere has radius 0.2 m and density 8 x 103 kg/m3. Find the moment of
inertia about the tangent to its surface. (π = 3.142)
A uniform solid sphere has a radius 0.1 m and density 6 x 103 kg/m3• Find its moment of inertia about a tangent to its surface.
A ballet dancer spins about a vertical axis at 2.5Π rad/s with his both arms outstretched. With the arms folded, the moment of inertia about the same axis of rotation changes by 25%. Calculate the new speed of rotation in r.p.m.
A thin ring has mass 0.25 kg and radius 0.5 m. Its moment of inertia about an axis passing through its centre and perpendicular to its plane is _______.
