Question

The corner points of the feasible region determined by the system of linear  constraints are as shown in the following figure:

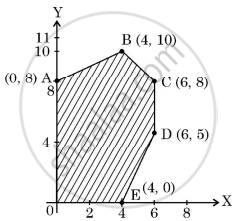
1. If Z = 3x  – 4y be the objective function, then find the maximum value of Z.
2. If Z = px + qy where p, q > 0 be the objective function. Find the condition on p and q so that maximum value of Z occurs at B (4, 10) and C (6, 8).

Answer 1

Given Z = 3x − 4y

(i) Z(A) = Z(0, 8) = 3 × 0 − 8 × 4 = −32

Z(B) = Z(4, 10) = 12 − 40 = −28

Z(C) = Z(6, 8) = 18 − 32 = −14

Z(D) = Z(6, 5) = 18 − 20 = −2

Z(E) = Z(4, 0) = 12 − 0 = −12

So, maximum value of Z = 12

(ii) Given Z = px + qy, where p, q > 0

Let Z be the maximum value of Z then it is given, maximum value of z occurs at B (4, 10) and C (6, 8)

⇒ Z₀ = p.4 + q.10

= p.6 + q.8

⇒ 4p + 10q = 6p + 8q

⇒ 2p = 2q

⇒ p = q

Hence, this is the required condition.