Advertisements
Advertisements
Question
The diagram below shows the path of a blue ray through the prism:
- Calculate the critical angle of the material of the prism for blue colour.
- What is the measure of the angle of this prism (A)?
- Which colour should replace the blue ray, for the ray to undergo Total Internal Reflection?

Solution
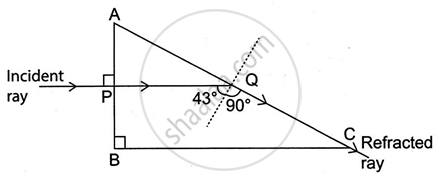
1. Here, the refracted ray PQ is normal to the surface AB of the prism (i.e., ∠r = 0°), so the incident ray at the point P should also be normal to the surface AB so that ∠i = 0°. At point Q, the angle of incidence for the ray PQ is 133° - 90° = 43°.
Now this angle should be equal to the critical angle because ray PQ is refracted at 90°, i.e., it is refracted along QC.
Hence, the critical angle of the prism is 43°.
2. In ΔAPQ
∠APQ + ∠PQA + ∠PAQ = 180°
90° + 47° + ∠PAQ = 180°
∠PAQ = 180° - 90° - 47°
∠PAQ = 43°
∴ ∠A = 43°
3. The light used and its wavelength determine the angle of deviation. With a decrease in the light wavelength, the angle of deviation increases.
Accordingly, the beam will experience total internal reflection if we swap out the blue light for intense light, sometimes known as indigo light.
APPEARS IN
RELATED QUESTIONS
Define the term angle of deviation.
Write a relation for the angle of deviation (δ) for a ray of light passing through an equilateral prism in terms of the angle of incidence (i1) angle of emergence (i2) and angle of the prism (A).
A ray of light is normally incident on one face of an equilateral glass prism. Answer the following:
Will the light ray suffer minimum deviation by the prism?
In following figure shows two identical prisms A and B placed with their faces parallel to each other. A ray of light of single colour PQ is incident at the face of the prism A. Complete the diagram to show the path of the ray till it emerges out of the prism B.
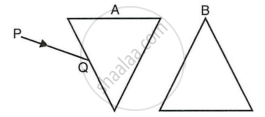
[Hint: The emergent ray out of the prism B will be parallel to the incident ray PQ]
In refraction of light through a prism, the light ray ______.
What should be the angle of incidence for a ray of light which suffers a minimum deviation of 36° through an equilateral prism?
[Hint: A = 60°, i = (A + δmin)/2]
In an experiment to trace the path of a ray of light through a glass prism for different values of angle of incidence a student would find that the emergent ray:
The diagram below shows the ray OP travelling through an equilateral prism of a certain material.
- Calculate the value of i2, if the angle of deviation is 43°.
- What is the ray QS called?
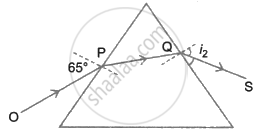
State three factors on which the angle of deviation depends.
