Advertisements
Advertisements
Question
The difference of three-digit number and the number obtained by putting the digits in reverse order is always divisible by 9 and ______.
Solution
The difference of three-digit number and the number obtained by putting the digits in reverse order is always divisible by 9 and 11.
Explanation:
Let abc be a three-digit number, then we have
abc – cba = (100a + 10b + c) – (100c + 10b + a)
= (100a – a) + (c – 100c)
= 99a – 99c
= 99(a – c)
= 9 × 11 × (a – c)
Hence, abc – cba is always divisible by 9, 11 and (a – c).
APPEARS IN
RELATED QUESTIONS
Without performing actual computations, find the quotient when 94 − 49 is divided by
(i) 9
(ii) 5
Find the quotient when the difference of 985 and 958 is divided by 9.
Which of the following statement is true?
If a number is divisible by 4, it must be divisible by 8.
Which of the following statement is true?
If a number exactly divides the sum of two numbers, it must exactly divide the numbers separately.
Which of the following statement is true?
If a number divides three numbers exactly, it must divide their sum exactly.
Which of the following statement is true?
If two numbers are co-prime, at least one of them must be a prime number.
Do you remember magic triangles? Come now, let s make some magic squares.
- Fill this square using all the numbers from 21 to 29.
Rule: The total of each side is 75.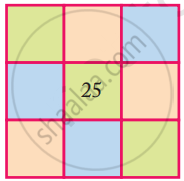
Use the same rule to fill the hexagons below.
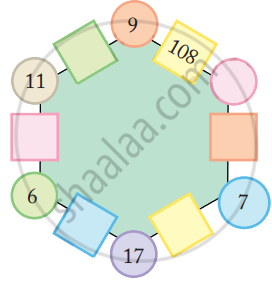
Now you also make your own magic hexagons.
If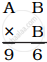 
then A = ______ and B = ______.
If a 3-digit number abc is divisible by 11, then ______ is either 0 or multiple of 11.
