Advertisements
Advertisements
Question
The distance (in km) of 40 engineers from their residence to their place of work were found as follows:-
| 5 | 3 | 10 | 20 | 25 | 11 | 13 | 7 | 12 | 31 |
| 19 | 10 | 12 | 17 | 18 | 11 | 32 | 17 | 16 | 2 |
| 7 | 9 | 7 | 8 | 3 | 5 | 12 | 15 | 18 | 3 |
| 12 | 14 | 2 | 9 | 6 | 15 | 15 | 7 | 6 | 12 |
Construct a grouped frequency distribution table with class size 5 for the data given above taking the first interval as 0-5 (5 not included). What main features do you observe from this tabular representation?
Solution
It is given that a grouped frequency distribution table of class size 5 has to be constructed. Therefore, the class intervals will be 0 − 5, 5 − 10, 10 − 15, 15 −20…
By observing the data given as above, a grouped frequency distribution table can be constructed as follows.
| Distance (in km) | Tally mark | Number of engineers |
| 0 − 5 | 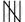 |
5 |
| 5 − 10 | 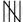 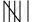 |
11 |
| 10 −15 |  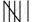 |
11 |
| 15 − 20 | 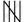  |
9 |
| 20 − 25 | | | 1 |
| 25 − 30 | | | 1 |
| 30 − 35 | || | 2 |
| Total | 40 |
It can be observed that there are very few engineers whose homes are at more than or equal to 20 km distance from their work place. Most of the engineers have their workplace up to 15 km distance from their homes.
APPEARS IN
RELATED QUESTIONS
Given below are the cumulative frequencies showing the weights of 685 students of a school. Prepare a frequency distribution table.
| Weight (in kg) | No. of students |
| Below 25 | 0 |
| Below 30 | 24 |
| Below 35 | 78 |
| Below 40 | 183 |
| Below 45 | 294 |
| Below 50 | 408 |
| Below 55 | 543 |
| Below 60 | 621 |
| Below 65 | 674 |
| Below 70 | 685 |
The following cumulative frequency distribution table shows the daily electricity consumption (in kW) of 40 factories in an industrial state:
| Consumption (in kW) | No. of Factories |
| Below 240 | 1 |
| Below 270 | 4 |
| Below 300 | 8 |
| Below 330 | 24 |
| Below 360 | 33 |
| Below 390 | 38 |
| Below 420 | 40 |
(i) Represent this as a frequency distribution table.
(ii) Prepare a cumulative frequency table.
In a frequency distribution, the mid-value of a class is 15 and the class intervals is 4. The lower limit of the class is
The mid-value of a class interval is 42. If the class size is 10, then the upper and lower limits of the class are:
The following marks were obtained by the students in a test:
81, 72, 90, 90, 86, 85, 92, 70, 71, 83, 89, 95, 85, 79, 62
The range of the marks is
Tallys are usually marked in a bunch of
The value of π upto 35 decimal places is given below:
3.14159265358979323846264338327950288
Make a frequency distribution of the digits 0 to 9 after the decimal point.
Prepare a continuous grouped frequency distribution from the following data:
| Mid-point | Frequency |
| 5 | 4 |
| 15 | 8 |
| 25 | 13 |
| 35 | 12 |
| 45 | 6 |
Also find the size of class intervals.
The following are the marks (out of 100) of 60 students in mathematics.
16, 13, 5, 80, 86, 7, 51, 48, 24, 56, 70, 19, 61, 17, 16, 36, 34, 42, 34, 35, 72, 55, 75, 31, 52, 28, 72, 97, 74, 45, 62, 68, 86, 35, 85, 36, 81, 75, 55, 26, 95, 31, 7, 78, 92, 62, 52, 56, 15, 63, 25, 36, 54, 44, 47, 27, 72, 17, 4, 30.
Construct a grouped frequency distribution table with width 10 of each class starting from 0 – 9.
The following are the marks (out of 100) of 60 students in mathematics.
16, 13, 5, 80, 86, 7, 51, 48, 24, 56, 70, 19, 61, 17, 16, 36, 34, 42, 34, 35, 72, 55, 75, 31, 52, 28, 72, 97, 74, 45, 62, 68, 86, 35, 85, 36, 81, 75, 55, 26, 95, 31, 7, 78, 92, 62, 52, 56, 15, 63, 25, 36, 54, 44, 47, 27, 72, 17, 4, 30.
Construct a grouped frequency distribution table with width 10 of each class, in such a way that one of the classes is 10 – 20 (20 not included).
