Advertisements
Advertisements
Question
The exterior angles, obtained on producing the side of a triangle both ways, are 100° and 120°. Find all the angles of the triangle.
Solution

∠ABP + ∠ABC = 180° ....(Linear pair)
⇒ 100° + ∠ABC = 180°
⇒ ∠ABC = 180° - 100° = 80°
∠ACQ + ∠ACB = 180° ....(Linear pair)
⇒ 120° + ∠ACB = 180°
⇒ ∠ACB = 180° - 120° = 60°
Now, in ΔABC,
∠A + ∠B + ∠C = 180° ....(Angle sum property of a triangle)
⇒ ∠A + 80° + 60° = 180°
⇒ ∠A = 180° - 80° - 60° = 40°
Hence, the angles of a triangle are 40°, 60° and 80°.
APPEARS IN
RELATED QUESTIONS
Use the given figure to find the value of x in terms of y. Calculate x, if y = 15°.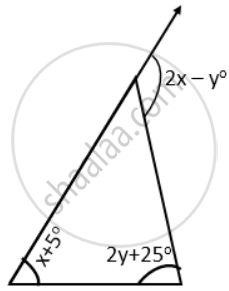
In a triangle PQR, ∠P + ∠Q = 130° and ∠P + ∠R = 120°. Calculate each angle of the triangle.
Use the given figure to find the value of y in terms of p, q and r.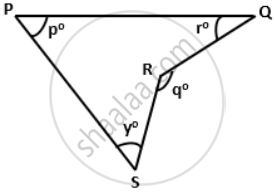
In the figure given below, if RS is parallel to PQ, then find the value of ∠y.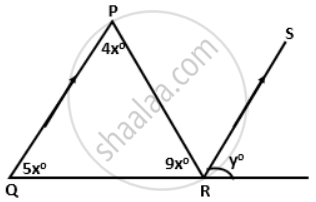
In a triangle PQR, the internal bisectors of angles Q and R meet at A and the external bisectors of the angles Q and R meet at B. Prove that: ∠QAR + ∠QBR = 180°.
Use the given figure to show that: ∠p + ∠q + ∠r = 360°.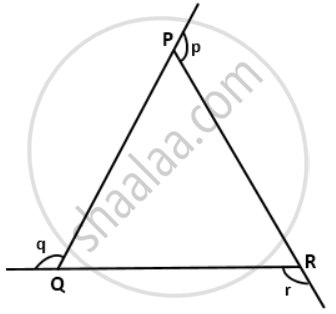
In a triangle ABC, if the bisectors of angles ABC and ACB meet at M then prove that: ∠BMC = 90° + `(1)/(2)` ∠A.
If bisectors of angles A and D of a quadrilateral ABCD meet at 0, then show that ∠B + ∠C = 2 ∠AOD
In a triangle, the sum of two angles is 139° and their difference is 5°; find each angle of the triangle.
In a right-angled triangle ABC, ∠B = 90°. If BA and BC produced to the points P and Q respectively, find the value of ∠PAC + ∠QCA.
