Advertisements
Advertisements
Question
In a triangle PQR, the internal bisectors of angles Q and R meet at A and the external bisectors of the angles Q and R meet at B. Prove that: ∠QAR + ∠QBR = 180°.
Solution

By exterior angle property,
∠RQS = ∠P + ∠R and ∠QRT = ∠P + ∠Q
Since QB bisects ∠RQS,
`∠"BQR" = (1)/(2)∠"RQS" = (1)/(2)(∠"P" + ∠"R")`
Also RB bisects ∠QRT,
`∠"BRQ" = (1)/(2)∠"QRT" = (1)/(2)(∠"P" + ∠"Q")`
In ΔQBR,
∠QBR + ∠BRQ + ∠BQR = 180°
⇒ `∠"QBR" + (1)/(2)(∠"P" + ∠"Q") + (1)/(2)(∠"P" + ∠"R")` = 180°
⇒ `∠"QBR" + (1)/(2)(∠"P" + ∠"Q" + ∠"P" + ∠"R")` = 180°
⇒ `∠"QBR" + (1)/(2)(∠"P" + 180°)` = 180° ....[∠P + ∠Q + ∠R = 180°]
⇒ 2∠QBR + ∠P + 180° = 360°
⇒ 2∠QBR = 180° - ∠P ....(i)
Since QB bisects ∠PQR,
∠AQR = `(1)/(2)∠"PQR"`
Also RA bisects ∠PRQ,
∠QRA = `(1)/(2)∠"PRQ"`
In ΔAQR,
∠AQR + ∠QRA + ∠QAR = 180°
⇒ `(1)/(2)∠"PQR" + (1)/(2)∠"PRQ" + ∠"QAR"` = 180°
⇒ `(1)/(2)(∠"PQR" + ∠"PRQ") + ∠"QAR"` = 180°
⇒ ∠PQR + ∠PRQ + 2∠QAR = 360°
⇒ 2∠QAR = 360° - ∠PQR - ∠PRQ
⇒ 2∠QAR = 180° + (180 - ∠PQR - ∠PRQ)
⇒ 2∠QAR = 180° + ∠P ....(ii)
Adding (i) and (ii)
⇒ 2∠QAR + 2∠QBR = 180° + ∠P + 180° - ∠P
⇒ 2∠QAR + 2∠QBR = 360°
⇒ ∠QAR + ∠QBR = 180°.
APPEARS IN
RELATED QUESTIONS
Use the given figure to find the value of x in terms of y. Calculate x, if y = 15°.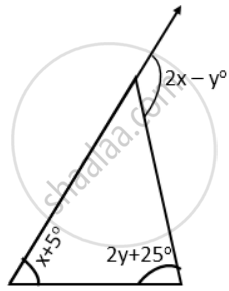
The angles of a triangle are (x + 10)°, (x + 30)° and (x - 10)°. Find the value of 'x'. Also, find the measure of each angle of the triangle.
In the figure given below, if RS is parallel to PQ, then find the value of ∠y.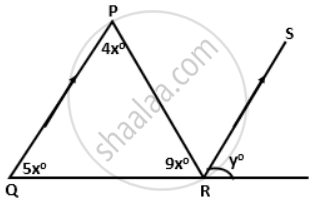
Use the given figure to show that: ∠p + ∠q + ∠r = 360°.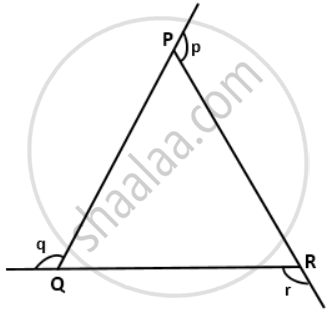
In a triangle ABC. If D is a point on BC such that ∠CAD = ∠B, then prove that: ∠ADC = ∠BAC.
In a triangle ABC, if the bisectors of angles ABC and ACB meet at M then prove that: ∠BMC = 90° + `(1)/(2)` ∠A.
If each angle of a triangle is less than the sum of the other two angles of it; prove that the triangle is acute-angled.
If the angles of a triangle are in the ratio 2: 4: 6; show that the triangle is a right-angled triangle.
In a triangle, the sum of two angles is 139° and their difference is 5°; find each angle of the triangle.
In a right-angled triangle ABC, ∠B = 90°. If BA and BC produced to the points P and Q respectively, find the value of ∠PAC + ∠QCA.
