Advertisements
Advertisements
प्रश्न
In a triangle PQR, the internal bisectors of angles Q and R meet at A and the external bisectors of the angles Q and R meet at B. Prove that: ∠QAR + ∠QBR = 180°.
उत्तर

By exterior angle property,
∠RQS = ∠P + ∠R and ∠QRT = ∠P + ∠Q
Since QB bisects ∠RQS,
`∠"BQR" = (1)/(2)∠"RQS" = (1)/(2)(∠"P" + ∠"R")`
Also RB bisects ∠QRT,
`∠"BRQ" = (1)/(2)∠"QRT" = (1)/(2)(∠"P" + ∠"Q")`
In ΔQBR,
∠QBR + ∠BRQ + ∠BQR = 180°
⇒ `∠"QBR" + (1)/(2)(∠"P" + ∠"Q") + (1)/(2)(∠"P" + ∠"R")` = 180°
⇒ `∠"QBR" + (1)/(2)(∠"P" + ∠"Q" + ∠"P" + ∠"R")` = 180°
⇒ `∠"QBR" + (1)/(2)(∠"P" + 180°)` = 180° ....[∠P + ∠Q + ∠R = 180°]
⇒ 2∠QBR + ∠P + 180° = 360°
⇒ 2∠QBR = 180° - ∠P ....(i)
Since QB bisects ∠PQR,
∠AQR = `(1)/(2)∠"PQR"`
Also RA bisects ∠PRQ,
∠QRA = `(1)/(2)∠"PRQ"`
In ΔAQR,
∠AQR + ∠QRA + ∠QAR = 180°
⇒ `(1)/(2)∠"PQR" + (1)/(2)∠"PRQ" + ∠"QAR"` = 180°
⇒ `(1)/(2)(∠"PQR" + ∠"PRQ") + ∠"QAR"` = 180°
⇒ ∠PQR + ∠PRQ + 2∠QAR = 360°
⇒ 2∠QAR = 360° - ∠PQR - ∠PRQ
⇒ 2∠QAR = 180° + (180 - ∠PQR - ∠PRQ)
⇒ 2∠QAR = 180° + ∠P ....(ii)
Adding (i) and (ii)
⇒ 2∠QAR + 2∠QBR = 180° + ∠P + 180° - ∠P
⇒ 2∠QAR + 2∠QBR = 360°
⇒ ∠QAR + ∠QBR = 180°.
APPEARS IN
संबंधित प्रश्न
The exterior angles, obtained on producing the side of a triangle both ways, are 100° and 120°. Find all the angles of the triangle.
Use the given figure to find the value of x in terms of y. Calculate x, if y = 15°.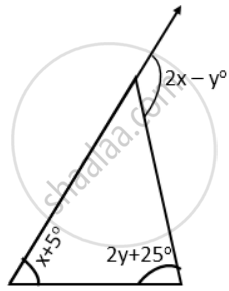
In a triangle PQR, ∠P + ∠Q = 130° and ∠P + ∠R = 120°. Calculate each angle of the triangle.
Use the given figure to find the value of y in terms of p, q and r.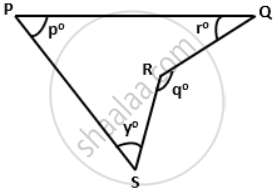
In the figure given below, if RS is parallel to PQ, then find the value of ∠y.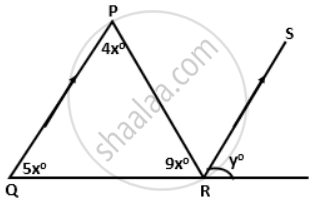
Use the given figure to show that: ∠p + ∠q + ∠r = 360°.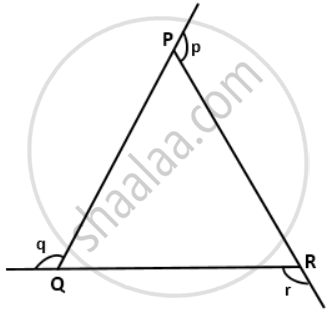
In a triangle ABC. If D is a point on BC such that ∠CAD = ∠B, then prove that: ∠ADC = ∠BAC.
If bisectors of angles A and D of a quadrilateral ABCD meet at 0, then show that ∠B + ∠C = 2 ∠AOD
In a triangle, the sum of two angles is 139° and their difference is 5°; find each angle of the triangle.
In a right-angled triangle ABC, ∠B = 90°. If BA and BC produced to the points P and Q respectively, find the value of ∠PAC + ∠QCA.
