Advertisements
Advertisements
प्रश्न
In a triangle PQR, ∠P + ∠Q = 130° and ∠P + ∠R = 120°. Calculate each angle of the triangle.
उत्तर

In ΔPQR,
∠P + ∠Q = 130° ....(given)
Now, ∠P + ∠Q = ∠PRY ....(Exterior angle property)
⇒ ∠PRY = 130°
∠PRY + ∠R = 180° ....(Linear pair)
⇒ 130° + ∠R = 180°
⇒ ∠R = 180° - 130° = 50°
Also, ∠P + ∠R = 120° ....(given)
Now, ∠P + ∠R = ∠PQX ....(Exeterior angle property)
⇒ ∠PQx = 120°
∠PQX +∠Q = 180° ....(Linear pair)
⇒ 120°+ ∠Q = 180°
⇒ ∠Q = 180° - 120° = 60°
In ΔPQR,
∠P + ∠Q + ∠R = 180° ....(Angle sum property of a triangle)
⇒ ∠P + 60° + 50° = 180°
⇒ ∠P = 180° - 110° = 70°
Thus, the angles of ΔPQR are as follows:
∠P = 70°, ∠Q = 60° and ∠R = 50°.
APPEARS IN
संबंधित प्रश्न
The exterior angles, obtained on producing the side of a triangle both ways, are 100° and 120°. Find all the angles of the triangle.
Use the given figure to find the value of x in terms of y. Calculate x, if y = 15°.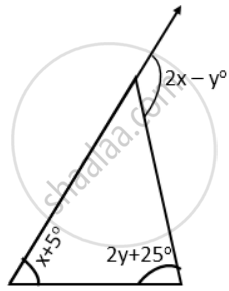
The angles of a triangle are (x + 10)°, (x + 30)° and (x - 10)°. Find the value of 'x'. Also, find the measure of each angle of the triangle.
In the figure given below, if RS is parallel to PQ, then find the value of ∠y.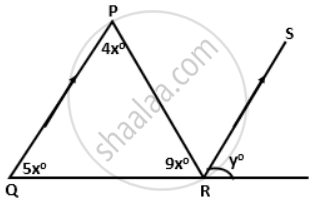
Use the given figure to show that: ∠p + ∠q + ∠r = 360°.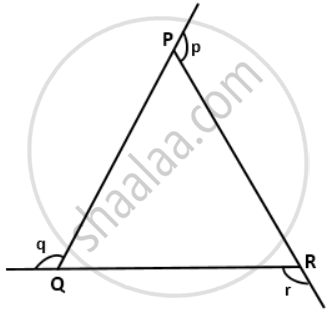
In a triangle ABC, if the bisectors of angles ABC and ACB meet at M then prove that: ∠BMC = 90° + `(1)/(2)` ∠A.
If bisectors of angles A and D of a quadrilateral ABCD meet at 0, then show that ∠B + ∠C = 2 ∠AOD
If the angles of a triangle are in the ratio 2: 4: 6; show that the triangle is a right-angled triangle.
In a triangle, the sum of two angles is 139° and their difference is 5°; find each angle of the triangle.
In a right-angled triangle ABC, ∠B = 90°. If BA and BC produced to the points P and Q respectively, find the value of ∠PAC + ∠QCA.
