Advertisements
Advertisements
प्रश्न
If bisectors of angles A and D of a quadrilateral ABCD meet at 0, then show that ∠B + ∠C = 2 ∠AOD
उत्तर

Since AO and DO are bisectors of ∠A and ∠D of quadrilateral ABCD,
∠A = 2∠OAD and ∠D = 2∠ODA ....(i)
In ΔAOD,
∠OAD + ∠ODA + ∠ACD = 180°
⇒ 2∠OAD + 2∠ODA + 2∠AOD = 360° ....[Multiplying both sides by 2]
⇒ 2∠OAD + 2∠ODA = 360° - 2∠AOD ....(ii)
In quadrlateral ABCD,
∠A + ∠B + ∠C + ∠D = 360°
⇒ 2∠OAD + ∠B + ∠C + 2∠ODA = 360° ....[From (i)]
⇒ ∠B + ∠C = 360° - 2∠OAD - 2∠ODA
⇒ ∠B + ∠C = 360° (2∠OAD + 2∠ODA)
⇒ ∠B + ∠C = 360° - (360° - 2∠AOD) ....[From (ii)]
⇒ ∠B + ∠C = 360° - 360° - 2∠AOD
⇒ ∠B + ∠C = 2∠AOD.
APPEARS IN
संबंधित प्रश्न
Use the given figure to find the value of x in terms of y. Calculate x, if y = 15°.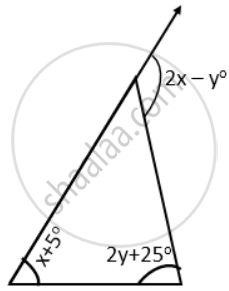
In a triangle PQR, ∠P + ∠Q = 130° and ∠P + ∠R = 120°. Calculate each angle of the triangle.
The angles of a triangle are (x + 10)°, (x + 30)° and (x - 10)°. Find the value of 'x'. Also, find the measure of each angle of the triangle.
Use the given figure to find the value of y in terms of p, q and r.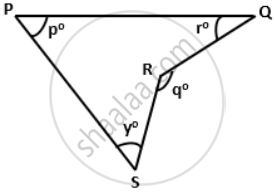
In a triangle PQR, the internal bisectors of angles Q and R meet at A and the external bisectors of the angles Q and R meet at B. Prove that: ∠QAR + ∠QBR = 180°.
Use the given figure to show that: ∠p + ∠q + ∠r = 360°.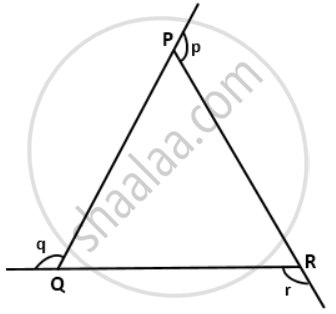
In a triangle ABC. If D is a point on BC such that ∠CAD = ∠B, then prove that: ∠ADC = ∠BAC.
In a triangle ABC, if the bisectors of angles ABC and ACB meet at M then prove that: ∠BMC = 90° + `(1)/(2)` ∠A.
If the angles of a triangle are in the ratio 2: 4: 6; show that the triangle is a right-angled triangle.
In a triangle, the sum of two angles is 139° and their difference is 5°; find each angle of the triangle.
