Advertisements
Advertisements
Question
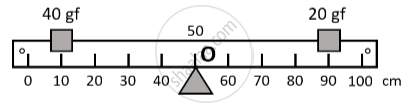
The figure shows a uniform metre rule placed on a fulcrum at its mid-point O and having a weight 40 gf at the 10 cm mark and a weight of 20 gf at the 90 cm mark.
- Is the metre rule in equilibrium? If not how will the rule turn?
- How can the rule be brought in equilibrium by using an additional weight of 40 gf?
Solution
W1 × d1 = W2 × d2
40 × 40 = 20 × 40
1600 ≠ 800
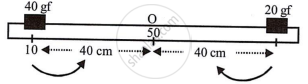
Anticlockwise moment ≠ clockwise moment
- No, the rule will turn anticlockwise
Anticlockwise moment > clockwise moment. - Moment of force needed = 800
Where 40 gf additional should be placed
1600 = 800 + 40 × d
∴ 40d = 1600 − 800 = 800
d = `800/40 = 20` cm
APPEARS IN
RELATED QUESTIONS
State two condition for a body acted upon by several forces to be in equilibrium.
State the principle of moments. A meter scale is pivoted at 30 cm mark and it is in equilibrium when a mass of 40 g is suspended from 10 cm mark. Calculate the mass of the ruler.
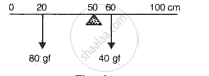
The arms of a beam balance are 20 cm and 21 cm, but the pans are of equal weight. By the method of double weighing the weights are found to be 1000 g and 20 g. Find the actual weight of the body
The moon revolving around the earth is in ______ equilibrium.
Explain when we carry weight, on one hand, we bend on the other side.
One end of a spring is kept fixed while the other end is stretched by a force as shown in the diagram.
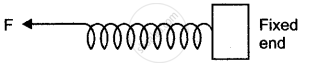
(i) Copy the diagram and mark on it the direction of the restoring force.
(ii) Name one instrument which works on the above principle.
A boy of mass 30 kg is fitting at a distance of 2 m from the middle of a see-saw. Where should a boy of mass 40 kg sit so as to balance the see-saw?
A ball is placed on a compressed spring. When the spring is released, the ball is observed to fly away.
(i) What form of energy does the compressed spring possess?
(ii) Why does the ball fly away?
