Advertisements
Advertisements
Question
The given figure shows a beam AB hinged at A and roller supported at B. The L shaped portion is welded at D to the beam AB. For the loading shown,find the support reactions.

Given : Beam AB hinged at A and roller supported at B and different forces acting on it.
To find : Support reactions
Solution
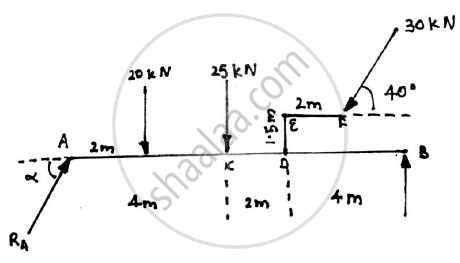
Force of distributed load AC = 5 x 4
= 20 kN
Distance of force acting from point A =` 4/2` =2m
The beam is in equilibrium
Applying the conditions of equilibrium
ΣMA = 0
-20 x 2 – 25 x 4 - 30sin40 x 8 + 30cos40 x 1.5 + RB x 10 = 0
10RB = 40 + 100 + 240sin40 - 45cos40
10RB = 259.797 kN
RB = 25.9797 kN (Acting upwards)
Applying the conditions of equilibrium
ΣFX = 0
RAX -30cos40 = 0
RAX = 22.9813 kN ………(1)
ΣFY = 0
RAY – 20 – 25 - 30sin40 + RB = 0
RAY= 38.3039 kN ………..(2)
`R_A = sqrt(R_(AX)^2 + R_(AY)^2 )`
`R_A = sqrt( 22.9813^2+38.3039^2)`
`R_A = 44.6691 kN`
`α =tan-1(R_(AY))/(R_(AX))`
`=tan-1(38.3039)/(22.9813)`
α=59.0374o
Reaction at hinge A = 44.6691 kN (59.0374o in first quadrant)
Reaction at roller B = 25.9797 kN (Towards up)
APPEARS IN
RELATED QUESTIONS
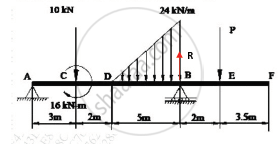
If the support reaction at A, for the beam shown in Figure 3, is zero, then find force ‘P’ and the support reaction at B.
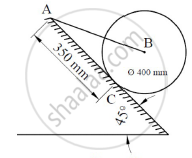
The cylinder B, diameter 400mm and weight 5kN, is held in position as shown in Figure 12 with the help of cable AB. Find the tension in the cable and the reaction developed at contact C.