Advertisements
Advertisements
Question
The image of triangle OXY under reflection in the origin, O is the triangle OX1Y1, where X1(-3, -4) is the image of X and Y1, (0, -5) is the image of Y.
(i) Draw a diagram to represent this information and write down the co-ordinates of X and Y.
(ii) What kind of figure is the quadrilateral XYX1Y1? Give reason for your answer. State, with a reason, whether the figure XYX1Y1 has any lines of symmetry.
(iii) Find the co-ordinates of X2, the image of X under reflection in the origin followed by reflection on the Y-axis.
(iv) Find the co-ordinates of Y2, the image of Y under reflection on the X-axis followed by reflection in the origin.
Solution
(i)
X1 → (-3, -4)
X → (3, 4)
Y1 → (0, -5)
Y → (0, 5).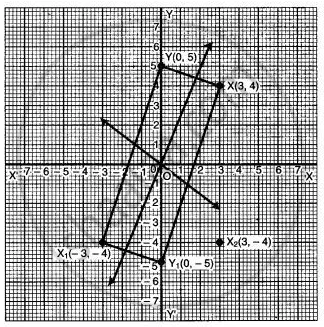
(ii) Rectangle.
Reasons : X1Y1 = YX
and X1Y1 = Y1X
Also each angle of the quadrilateral XYX1Y1 is 90°.
It has two lines of symmetry. These are the perpendicular bisectors of each pair of opposite sides.
(iii) X2 = (3, -4).
(iv) Y2 = (0, 5).
APPEARS IN
RELATED QUESTIONS
State the co-ordinates of the following point under reflection in origin:
(–2, –4)
The point A(4, 6) is first reflected in the origin to point A’. Point A’ is then reflected in the y-axis to the point A”.
- Write down the co-ordinates of A”.
- Write down a single transformation that maps A onto A”.
The triangle ABC, where A is (2, 6), B is (-3, 5) and C is (4, 7), is reflected in the y-axis to triangle A’B’C’. Triangle A’B’C’ is then reflected in the origin to triangle A”B”C”.
(i) Write down the co-ordinates of A”, B” and C”.
(ii) Write down a single transformation that maps triangle ABC onto triangle A”B”C”.
On a graph paper, plot the triangle ABC, whose vertices are at the points A (3, 1), B (5, 0) and C (7, 4).
On the same diagram, draw the image of the triangle ABC under reflection in the origin O (0, 0).
Find the image of point (4, -6) under the following operations:
(i) Mx . My (ii) My . Mx
(iii) MO . Mx (iv) Mx . MO
(v) MO . My (vi) My . MO
Write down a single transformation equivalent to each operation given above. State whether:
(a) MO . Mx = Mx . MO
(b) My . MO = MO . My
The point (–5, 0) on reflection in a line is mapped as (5, 0) and the point (–2, –6) on reflection in the same line is mapped as (2, –6).
- Name the line of reflection.
- Write down the co-ordinates of the image of (5, –8) in the line obtained in (a).
State the co-ordinates of the images of the following point under reflection in the origin:
(9,-9)
Find the co-ordinates of the images of the following under reflection in the origin:
(3, -7)
Find the co-ordinates of the images of the following under reflection in the origin:
`((-5)/(2),(-1)/(2))`
Find the co-ordinates of the images of the following under reflection in the origin:
(0, 0).
