Advertisements
Advertisements
प्रश्न
The image of triangle OXY under reflection in the origin, O is the triangle OX1Y1, where X1(-3, -4) is the image of X and Y1, (0, -5) is the image of Y.
(i) Draw a diagram to represent this information and write down the co-ordinates of X and Y.
(ii) What kind of figure is the quadrilateral XYX1Y1? Give reason for your answer. State, with a reason, whether the figure XYX1Y1 has any lines of symmetry.
(iii) Find the co-ordinates of X2, the image of X under reflection in the origin followed by reflection on the Y-axis.
(iv) Find the co-ordinates of Y2, the image of Y under reflection on the X-axis followed by reflection in the origin.
उत्तर
(i)
X1 → (-3, -4)
X → (3, 4)
Y1 → (0, -5)
Y → (0, 5).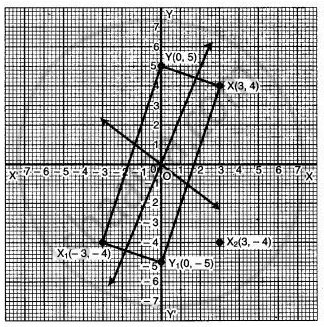
(ii) Rectangle.
Reasons : X1Y1 = YX
and X1Y1 = Y1X
Also each angle of the quadrilateral XYX1Y1 is 90°.
It has two lines of symmetry. These are the perpendicular bisectors of each pair of opposite sides.
(iii) X2 = (3, -4).
(iv) Y2 = (0, 5).
APPEARS IN
संबंधित प्रश्न
A point P is reflected in the origin. Co-ordinates of its image are (–2, 7). Find the co-ordinates of P.
The point A(4, 6) is first reflected in the origin to point A’. Point A’ is then reflected in the y-axis to the point A”.
- Write down the co-ordinates of A”.
- Write down a single transformation that maps A onto A”.
P and Q have co-ordinates (–2, 3) and (5, 4) respectively. Reflect P in the x-axis to P’ and Q in the y-axis to Q’. State the co-ordinates of P’ and Q’.
Find the image of point (4, -6) under the following operations:
(i) Mx . My (ii) My . Mx
(iii) MO . Mx (iv) Mx . MO
(v) MO . My (vi) My . MO
Write down a single transformation equivalent to each operation given above. State whether:
(a) MO . Mx = Mx . MO
(b) My . MO = MO . My
Point A (4, –1) is reflected as A’ in the y-axis. Point B on reflection in the x-axis is mapped as B’ (–2, 5). Write down the co-ordinates of A’ and B.
State the co-ordinates of the images of the following point under reflection in the origin:
(-1,-4)
State the co-ordinates of the images of the following point under reflection in the origin:
(9,-9)
Find the co-ordinates of the images of the following under reflection in the origin:
(3, -7)
Find the co-ordinates of the images of the following under reflection in the origin:
`((-5)/(2),(-1)/(2))`
Point A (2, -4) is reflected in origin as A’. Point B (- 3, 2) is reflected on X-axis as B’.
(i) Write the co-ordinates of A’.
(ii) Write the co-ordinates of B’.
(iii) Calculate the distance A’B’.
Give your answer correct to 1 decimal place, (do not consult tables).
