Advertisements
Advertisements
Question
The length , breadth and height of a room are 5 m, 4.5 m and 3 m, respectively. Find the volume of the air it contains.
Solution
Length of the room = 5 m
Breadth = 4 . 5 m
Height = 3 m
\[\text { Now, volume = length } \times \text { breadth }\times \text { height }\]
\[ = 5 \times 4 . 5 \times 3\]
\[ = 67 . 5 m^3 \]
\[ \therefore \text { The volume of air in the room is 67 . 5 }m^3 .\]
APPEARS IN
RELATED QUESTIONS
A small indoor greenhouse (herbarium) is made entirely of glass panes (including base) held together with tape. It is 30 cm long, 25 cm wide and 25 cm high. What is the area of the glass?
A solid rectangular piece of iron measures 6 m by 6 cm by 2 cm. Find the weight of this piece, if 1 cm3 of iron weighs 8 gm.
Find the surface area of a cuboid whose length = 10 cm, breadth = 12 cm, height = 14 cm.
If V is the volume of a cuboid of dimensions a, b, c and S is its surface area, then prove that \[\frac{1}{V} = \frac{2}{S}\left( \frac{1}{a} + \frac{1}{b} + \frac{1}{c} \right)\]
The sum of the length, breadth and depth of a cuboid is 19 cm and its diagonal is ` 5 sqrt(5)` cm. Its surface area is
If V is the volume of a cuboid of dimensions x, y, z and A is its surface area, then `A/V`
If radii of two cylinders are in the ratio 4 : 3 and their heights are in the ratio 5: 6, find the ratio of their curved surfaces.
Find the volume of a cuboid whose diagonal is `3sqrt(29)"cm"` when its length, breadth and height are in the ratio 2 : 3 : 4.
A square plate of side 'x' cm is 4 mm thick. If its volume is 1440 cm3; find the value of 'x'.
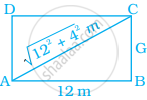
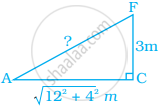
Find the length of the largest pole that can be placed in a room of dimensions 12 m × 4 m × 3 m.