Advertisements
Advertisements
Question
The mark of 200 students in a test were recorded as follows:
| Marks % | No. of students |
| 10 - 19 | 7 |
| 20 - 29 | 11 |
| 30 - 39 | 20 |
| 40 - 49 | 46 |
| 50 - 59 | 57 |
| 60 - 69 | 37 |
| 70 - 79 | 15 |
| 80 - 89 | 7 |
Draw the cumulative frequency table.
Draw an ogive and use it to find:
(i) The median
(ii) The number of students who scored more than 35% marks.
Solution
The given frequency distribution is discontinuous, to convert it into continuous distribution.
Adjustment factor = `(20 - 19)/(2)` = 0·5.
Cumulative (continuous) frequency tab;e for the given data is :
| Marks % (Classes before adjustment) |
Marks % (Classes after adjustment) |
Frequency | Cumulative frequency |
| 10 - 19 | 9·5 - 19·5 | 7 | 7 |
| 20 - 29 | 19·5 - 29·5 | 11 | 18 |
| 30 - 39 | 29·5 - 39·5 | 20 | 38 |
| 40 - 49 | 39·5 - 49·5 | 46 | 84 |
| 50 - 59 | 49·5 - 59·5 | 57 | 141 |
| 60 - 69 | 59·5 - 69·5 | 37 | 178 |
| 70 - 79 | 69·5 - 79·5 | 15 | 193 |
| 80 - 89 | 79·5 - 89·5 | 7 | 200 |
Take 1 cm along X-axis = 10% marks and 1 cm along Y-axis = 25 students.
Plot the point (19·5, 7), (29·5 - 18), (39·5 - 38), (49·5 - 141), (69·5 - 178), (9·5 - 193), (89·5 - 200) and (9·5 - 0) join these points by a free hand drawing.
The required ogive is drawn in the figure given below: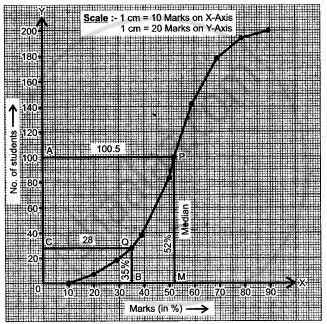
(i) To find the median: Let A be a point on Y-axis representing frequency
= `(1)/(2) [("n"^"th"/2 "term") + ("n"/2 + 1)^"th" "term"]`
= `(1)/(2)(100 + 101)`
= 100·5.
Through A draw a horizontal line to meet the ogive at P. Through P draw a vertical line to meet X-axis at M. the abscissae of point M represents 52%.
∴ The required median = 52%.
(ii) Let the point B on X-axis represent 35% marks. Through B draw a vertical line to meet the ogive at Q. Through Q draw a horizontal line to meet Y-axis at C. The ordinate of the point C represents 28 students on Y-axis.
∴ The number of students who scored more than 35% marks = total no. of students - no. of students who scored ≤35%
= 200 - 8
= 172.
APPEARS IN
RELATED QUESTIONS
The table shows the distribution of the scores obtained by 160 shooters in a shooting competition. Use a graph sheet and draw an ogive for the distribution. (Take 2 cm = 10 scores on the X-axis and 2 cm = 20 shooters on the Y-axis).
| Scores | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 | 60-70 | 70-80 | 80-90 | 90-100 |
| No. of shooters |
9 | 13 | 20 | 26 | 30 | 22 | 15 | 10 | 8 | 7 |
Use your graph to estimate the following:
1) The median
2) The interquartile range.
3) The number of shooters who obtained a score of more than 85%.
The marks obtained by 120 students in a test are given below:
| Marks | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 | 60-70 | 70-80 | 80-90 | 90-100 |
| No. of students |
5 | 9 | 16 | 22 | 26 | 18 | 11 | 6 | 4 | 3 |
Draw an ogive for the given distribution on a graph sheet.
Use a suitable scale for ogive to estimate the following:
(1) The median.
(2) The number of students who obtained more than 75% marks in the test.
(3) The number of students who did not pass the test if minimum marks required to pass is 40
Construct a frequency distribution table for the numbers given below, using the class intervals 21-30, 31-40, ... etc.
75, 65, 57, 26, 33, 44, 58, 67, 75, 78, 43, 41, 31, 21, 32, 40, 62, 54, 69, 48, 47, 51, 38, 39, 43, 61, 63, 68, 53, 56, 49, 59, 37, 40, 68, 23, 28, 36 and 47.
Use the table obtained to draw:
- a histrogram
- an ogive
| Class mark | 12.5 | 17.5 | 22.5 | 27.5 | 32.5 | 37.5 | 42.5 |
| Frequency | 12 | 17 | 22 | 27 | 30 | 21 | 16 |
- From the distribution, given above, construct a frequency table.
- Use the table obtained in part (a) to draw : (i) a histogram, (ii) an ogive.
Use graph paper for this question.
The table given below shows the monthly wages of some factory workers.
- Using the table, calculate the cumulative frequencies of workers.
- Draw a cumulative frequency curve.
Use 2 cm = ₹ 500, starting the origin at ₹ 6500 on x-axis, and 2 cm = 10 workers on the y-axis.
| Wages (in ₹.) | 6500-7000 | 7000-7500 | 7500-8000 | 8000-8500 | 8500-9000 | 9000-9500 | 9500-10000 |
| No. of workers | 10 | 18 | 22 | 25 | 17 | 10 | 8 |
Marks obtained by 200 students in an examination are given below:
| Marks | 0 - 10 | 10 - 20 | 20 - 30 | 30 - 40 | 40 - 50 | 50 - 60 | 60 - 70 | 70 - 80 | 80 - 90 | 90 - 100 |
| Frequency | 5 | 11 | 10 | 20 | 28 | 37 | 40 | 29 | 14 | 6 |
Draw an ogive for the given distribution taking 2 cm = 10 marks on one axis and 2 cm = 20 students on the other axis. Using the graph, determine:
(i) The median marks
(ii) The number of students who failed if minimum marks required to pass is 40.
(iii) If scoring 85 and more marks is considered as grade one, find the number of students who secured grade one in the examination.
Attempt this question on graph paper. Marks obtained by 200 students in examination are given below:
| Marks | 0 - 10 | 10 - 20 | 20 - 30 | 30 - 40 | 40 - 50 | 50 - 60 | 60 - 70 | 70 - 80 | 80 - 90 | 90 - 100 |
| No. of students | 5 | 10 | 14 | 21 | 25 | 34 | 36 | 27 | 16 | 12 |
Draw an ogive for the given distribution taking 2 cm = 10 makrs on one axis and 2 cm = 20 students on the other axis.
From the graph find:
(i) the median
(ii) the upper quartile
(iii) number of student scoring above 65 marks.
(iv) If to students qualify for merit scholarship, find the minimum marks required to qualify.
The daily wages of 160 workers in a building project are given below:
| Wages in ₹ | 0 - 10 | 10 - 20 | 20 - 30 | 30 - 40 | 40 - 50 | 50 - 60 | 60 - 70 | 70 - 80 |
| No. of Workers | 12 | 20 | 30 | 38 | 24 | 16 | 12 | 8 |
Using a graph paper, draw in Ogive for the above distribution.
Use your Ogive to estimate :
(i) the median wage of the workers.
(ii) the upper quartile wage of the workers
(iii) the lower quartile wages of the workers
(iv) the percentage of workers who earn more than ₹ 45 a day.
The marks obtained by 120 students in a test are given below:
| Marks | 0 - 10 | 10 - 20 | 20 - 30 | 30 - 40 | 40 - 50 | 50 - 60 | 60 - 70 | 70 - 80 | 80 - 90 | 90 - 100 |
| No. of Students | 5 | 9 | 16 | 22 | 26 | 18 | 11 | 6 | 4 | 3 |
Draw an ogive for the given distribution on a graph sheet.
Use suitable scale for ogive to estimate the following :
(i) the median.
(ii) The number of students who obtained more than 75% marks in the test.
The marks obtained by 100 students in a Mathematics test are given below:
| Marks | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 | 60-70 | 70-80 | 80-90 | 90-100 |
| No. of Students | 3 | 7 | 12 | 17 | 23 | 14 | 9 | 6 | 5 | 4 |
Draw an ogive for the given distribution on a graph sheet.
Use a scale of 2 cm = 10 units on both axes.
Use the ogive to estimate the :
- median.
- lower quartile.
- number of students who obtained more than 85% marks in the test.
- number of students who did not pass in the test if the pass percentage was 35.
