Advertisements
Advertisements
Question
The number of lines of symmetry in a 30° – 60° – 90° set square is ______.
Options
0
1
2
3
Solution
The number of lines of symmetry in a 30° – 60° – 90° set square is 0.
Explanation:
The set-square of measurement 30° – 60° – 90° is in the shape of a scalene right-angled triangle which has no line of symmetry.
APPEARS IN
RELATED QUESTIONS
Construct an isosceles triangle whose equal sides are 7 cm each and the base side is 5 cm. Draw all its lines of symmetry.
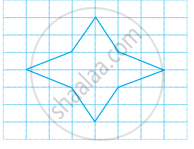
Draw the line of symmetry of the following figure and also mark their points of symmetry, if any:
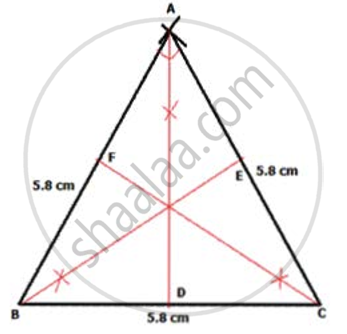
Construct a triangle ABC in which each side measures 5.8 cm. Draw all the possible lines of symmetry.
Construct a Δ ABC in whidi BA= BC= 6 cm and AC= 4.5 cm. Taking AC as line of symmetry, obtain a point D to form a quadrilateral ABCD. Name the figure ABCD.
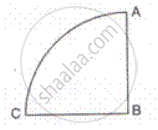
Draw a line of symmetry of the given figure such that one hole coincide with the other hole(s) to make pairs.
Which of the following letter does not have a line of symmetry?
Can you see that this shape looks the same on the `1/6` turn?

Copy the triangle in the following figure on squared paper. Draw the line(s) of symmetry, if any and identify the type of triangle. (Some of you may like to trace the figure and try paper-folding first!)
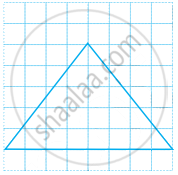
Can you draw a triangle which has exactly two lines of symmetry?
Trace the figure and draw the lines of symmetry, if any: