Advertisements
Advertisements
Question
The number of sides in a regular polygon having measure of an exterior angle as 72° is ______.
Solution
The number of sides in a regular polygon having measure of an exterior angle as 72° is 5.
Explanation:
We know that, the sum of exterior angles of any polygon is 360°.
The number of sides in a regular polygon = `360^circ/"Exterior angle"`
∴ The number of sides in given polygon = `360^circ/72^circ` = 5
APPEARS IN
RELATED QUESTIONS

The sum of all exterior angles of a triangle is ______.
The number of sides of a regular polygon where each exterior angle has a measure of 45° is ______.
The number of sides of a regular polygon, where each exterior angle has a measure of 36°, is ______.
Triangle is a polygon whose sum of exterior angles is double the sum of interior angles.
The sum of interior angles and the sum of exterior angles taken in an order are equal in case of quadrilaterals only.
The ratio between exterior angle and interior angle of a regular polygon is 1:5. Find the number of sides of the polygon.
In the figure, find the value of x.
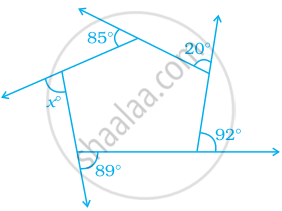
Find maximum number of acute angles which a convex, a quadrilateral, a pentagon and a hexagon can have. Observe the pattern and generalise the result for any polygon.
