Advertisements
Advertisements
Question
The points A(x1, y1), B(x2, y2) and C(x3, y3) are the vertices of ∆ABC. Find the coordinates of points Q and R on medians BE and CF, respectively such that BQ : QE = 2 : 1 and CR : RF = 2 : 1
Solution
According to the question,
The vertices of ΔABC = A, B and C
Coordinates of A, B and C = A(x1, y1), B(x2, y2), C(x3, y3)
Let the coordinates of a point Q be (p, q)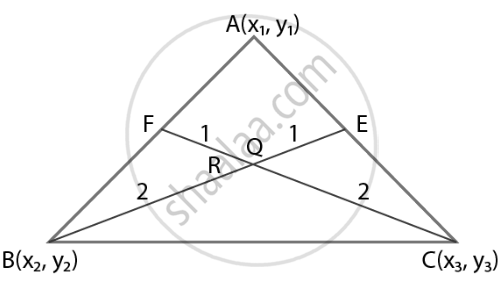
Given,
The point Q(p, q),
Divide the line joining `"B"(x_2, y_2)` and `"E"((x_1 + x_3)/2, (y_1 + y_3)/2)` in the ratio 2 : 1,
Then,
Coordinates of Q = `[(2 xx ((x_1 + x_3)/2) + 1 xx x_2)/(2 + 1), (2 xx ((y_1 + y_3)/2) + 1 xx y_2)/(2 + 1)]`
= `((x_1 + x_2 + x_3)/3, (y_1 + y_2 + y_3)/3)`
Since, BE is the median of side CA,
So BE divides AC into two equal parts.
∴ Mid-point of AC = Coordinate of E;
E = `((x_1 + x_3)/2, (y_1 + y_3)/2)`
So, the required coordinate of point Q;
Q = `((x_1 + x_2 + x_3)/3, (y_1 + y_2 + y_3)/3)`
Now,
Let the coordinates of a point E be (⍺, β)
Given,
Point `"R"(alpha, beta)` divide the line joining `"C"(x_3, y_3)` and `"F"((x_1 + x_2)/2, (y_1 + y_2)/2)` in the ratio 2 : 1,
Then the coordinates of R;
= `[(2 xx ((x_1 + x_2)/2) + 1 xx x_3)/(2 + 1), (2 xx ((y_1 + y_2)/2) + 1 xx y_3)/(2 + 1)]`
= `((x_1 + x_2 + x_3)/3, (y_1 + y_2 + y_3)/3)`
Since, CF is the median of side AB.
So, CF divides AB into two equal parts.
∴ Mid-point of AB = Coordinates of F;
F = `((x_1 + x_2)/2, (y_1 + y_2)/2)`
So, the required coordinate of point R;
= `((x_1 + x_2 + x_3)/3, (y_1 + y_2 + y_3)/3)`
APPEARS IN
RELATED QUESTIONS
If A(–2, –1), B(a, 0), C(4, b) and D(1, 2) are the vertices of a parallelogram, find the values of a and b
Find the coordinates of the points of trisection of the line segment joining (4, -1) and (-2, -3).
Find the ratio in which the line segment joining the points (-3, 10) and (6, -8) is divided by (-1, 6).
If two vertices of a parallelogram are (3, 2) (-1, 0) and the diagonals cut at (2, -5), find the other vertices of the parallelogram.
The line segment joining the points (3, -4) and (1, 2) is trisected at the points P and Q. If the coordinates of P and Q are (p, -2) and (5/3, q) respectively. Find the values of p and q.
Find the co-ordinates of the points of tri-section of the line joining the points (–3, 0) and (6, 6).
- Write down the co-ordinates of the point P that divides the line joining A(−4, 1) and B(17, 10) in the ratio 1 : 2.
- Calculate the distance OP, where O is the origin.
- In what ratio does the y-axis divide the line AB?
The three vertices of a parallelogram ABCD are A(3, −4), B(−1, −3) and C(−6, 2). Find the coordinates of vertex D and find the area of ABCD.
A (30, 20) and B ( 6, -4) are two fixed points. Find the coordinates of a point Pin AB such that 2PB = AP. Also, find the coordinates of some other point Qin AB such that AB = 6 AQ.
Find the ratio in which the x-axis divides internally the line joining points A (6, -4) and B ( -3, 8).
