Advertisements
Advertisements
Question
The radius of two right circular cylinder are in the ratio of 2 : 3 and their heights are in the ratio of 5: 4 calculate the ratio of their curved surface areas and also the ratio of their volumes.
Solution
Let the radii of two cylinders be 2r and 3r respectively and their heights be 5h and 4h respectively.
Let S1 and S2 be Curved Surface Area of the two cylinders and V1 and V2 be their volumes.
Then, S1 = Curved surface area of the cylinders of height 5h and radius 2r.
⇒ 2π x 2r x 5h = 20πrh sq. units.
S2 = Curved surface area of the cylinders of height 4h and radius 3r.
⇒ 2π x 3r x 4h = 24πrh sq. units.
`S_1/S_2 = (20πrh)/(24πrh) = 5/6`
S1: S2 = 5: 6
V1 = Volume of cylinder of height 5h and radius 2r
= π x (2r)2 x 5h = 20πr2h cubic units.
V2 = Volume of the cylinder of height 4h and radius 3r.
= π x (3r)2 x 4h = 36πr2h cubic units.
∴ `V_1/V_2 = (20πr^2h)/(36πr^2h) = 5/6`
V1: V2 = 5: 9.
APPEARS IN
RELATED QUESTIONS
How many cubic meters of earth must be dug out to make a well 28 m deep and 2.8 m in diameter ? Also, find the cost of plastering its inner surface at Rs 4.50 per sq meter.
3080 cm3 of water is required to fill a cylindrical vessel completely and 2310 cm3 of water is required to fill it upto 5 cm below the top. Find :
- radius of the vessel.
- height of the vessel.
- wetted surface area of the vessel when it is half-filled with water.
Find the volume of the largest cylinder formed when a rectangular piece of paper 44 cm by 33 cm is rolled along it : longer side.
Water flows through a cylindrical pipe of internal diameter 7 cm at 36 km/hr. Calculate the time in minutes it would take to fill the cylindrical tank, the radius of whose base is 35 cm, and height is 1 m.
A rectangular paper of width 14 cm is rolled along its width and a cylinder of radius 20 cm is formed. Find the volume of the cylinder. (Take `22/7` for π)

The ratio of the volumes of a cylinder, a cone and a sphere, if each has the same diameter and same height is
A cylindrical tube opened at both the ends is made of iron sheet which is 2 cm thick. If the outer diameter is 16 cm and its length is 100 cm, find how many cubic centimeters of iron has been used in making the tube?
The volume of a cylinder whose radius r is equal to its height is ______.
A rectangular sheet of paper is rolled in two different ways to form two different cylinders. Find the volume of cylinders in each case if the sheet measures 44 cm × 33 cm.
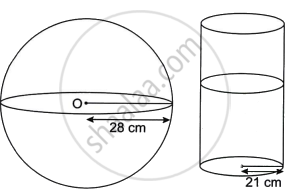
Oil is stored in a spherical vessel occupying `3/4` of its full capacity. Radius of this spherical vessel is 28 cm. This oil is then poured into a cylindrical vessel with a radius of 21 cm. Find the height of the oil in the cylindrical vessel (correct to the nearest cm). Take π = `22/7`