Advertisements
Advertisements
Question
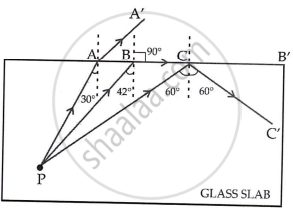
The refractive index of glass is 1.5. From a point P inside a glass block, draw rays PA, PB and PC incident on the glass air surface at an angle of incidence 30°, 42° and 60° respectively.
- In the diagram show the approximate direction of these rays as they emerge out of the block.
- What is the angle of refraction for the ray PB?
`("Take" sin 42° =2/3)`
Solution
- A diagram with rays PA, PB and PC is shown below:
- Given, μ = 1.5
As we know,
`sin i_c = 1/mu`
substituting the values in the formula, we get,
`sin i_c = 1/1.5`
sin ic = 0.667
ic = 41.8
Hence, we can round off ic = 42°
Applying `sin r/sin i = ""_amu_g`
sin r = `""_amu_g xx sin i`
sin r = `""_amu_g xx sin 42°`
Given, sin 42° = `2/3`
and `""_amu_g = 3/2`
substituting the value in the formula, we get,
`sin r = 3/2 xx 2/3`
sin r = 1
As sin r = 1, the angle of refraction is 90°.
APPEARS IN
RELATED QUESTIONS
Name a prism required for obtaining a spectrum of Ultraviolet light.
How is the reflection of light ray from a plane mirror different from the refraction of light ray as it enters a block of glass?
When a ray of light from air enters a denser medium, it ______.
A Water pond appears to be 2.7 m deep. If the refractive index of water is 4/3, find the actual depth of the pond.
Trace the path of a ray of light incident at an angle of 45° on a rectangular glass slab. Write the measure of the angle of refraction, the angle of emergence and the lateral displacement suffered by the ray as it passes through the slab.
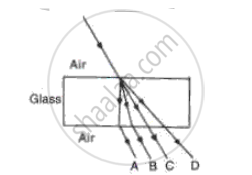
In the fig. name the ray which represents the correct path of light while passing through a glass block.
Does the depth of a tank of water appear to change or remain the same when viewed normally from above?
Write a relation between the angle of incidence (i), angle of emergence (e), angle of the prism (A), and angle of deviation (d) for a ray of light passing through an equilateral prism.
Calculate the velocity of light in a glass block of refractive index 1.5. (Velocity of light in air = 3 × 108 m/s)