Advertisements
Advertisements
Question
The rotation of earth about its axis is ______.
- periodic motion.
- simple harmonic motion.
- periodic but not simple harmonic motion.
- non-periodic motion.
Solution
a and c
Explanation:
The motion of earth about its own axis is circular motion and completes its one complete revolution in a regular interval of time. So the motion is said to be periodic. But motion is not about a fixed point from which we can measure its displacement or about which it moves both sides so it is not simple harmonic motion.
APPEARS IN
RELATED QUESTIONS
The motion of a particle executing simple harmonic motion is described by the displacement function,
x (t) = A cos (ωt + φ).
If the initial (t = 0) position of the particle is 1 cm and its initial velocity is ω cm/s, what are its amplitude and initial phase angle? The angular frequency of the particle is π s–1. If instead of the cosine function, we choose the sine function to describe the SHM: x = B sin (ωt + α), what are the amplitude and initial phase of the particle with the above initial conditions.
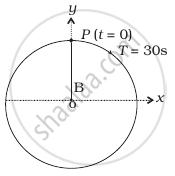
Figures correspond to two circular motions. The radius of the circle, the period of revolution, the initial position, and the sense of revolution (i.e. clockwise or anti-clockwise) are indicated on each figure

Obtain the corresponding simple harmonic motions of the x-projection of the radius vector of the revolving particle P, in each case.
Figure (a) shows a spring of force constant k clamped rigidly at one end and a mass m attached to its free end. A force F applied at the free end stretches the spring. Figure (b) shows the same spring with both ends free and attached to a mass mat either end. Each end of the spring in Fig. (b) is stretched by the same force F.
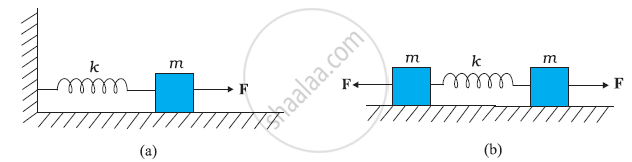
(a) What is the maximum extension of the spring in the two cases?
(b) If the mass in Fig. (a) and the two masses in Fig. (b) are released, what is the period of oscillation in each case?
Which of the following functions of time represent (a) simple harmonic, (b) periodic but not simple harmonic, and (c) non-periodic motion? Give period for each case of periodic motion (ω is any positive constant):
sin ωt – cos ωt
Which of the following functions of time represent (a) simple harmonic, (b) periodic but not simple harmonic, and (c) non-periodic motion? Give period for each case of periodic motion (ω is any positive constant):
sin3 ωt
Which of the following functions of time represent (a) simple harmonic, (b) periodic but not simple harmonic, and (c) non-periodic motion? Give period for each case of periodic motion (ω is any positive constant):
3 cos `(π/4 – 2ω"t")`
Which of the following functions of time represent (a) simple harmonic, (b) periodic but not simple harmonic, and (c) non-periodic motion? Give period for each case of periodic motion (ω is any positive constant):
cos ωt + cos 3ωt + cos 5ωt
Which of the following functions of time represent (a) simple harmonic, (b) periodic but not simple harmonic, and (c) non-periodic motion? Give period for each case of periodic motion (ω is any positive constant):
1 + ωt + ω2t2
A particle is acted simultaneously by mutually perpendicular simple harmonic motions x = a cos ωt and y = a sin ωt. The trajectory of motion of the particle will be ______.
Figure shows the circular motion of a particle. The radius of the circle, the period, sense of revolution and the initial position are indicated on the figure. The simple harmonic motion of the x-projection of the radius vector of the rotating particle P is ______.