Advertisements
Advertisements
Question
The sum of ages of a man and his son is 45 years. Five years ago, the product of their ages was four times the man's age at the time. Find their present ages.
Solution
Let the present age of the man be x years
Then present age of his son is (45 - x) years
Five years ago, man’s age = (x - 5) years
And his son’s age (45 - x - 5) = (40 - x) years
Then according to question,
(x - 5)(40 - x) = 4(x - 5)
40x - x2 + 5x - 200 = 4x - 20
-x2 + 45x - 200 = 4x - 20
-x2 + 45x - 200 - 4x + 20 = 0
-x2 + 41x - 180 = 0
x2 - 41x + 180 = 0
x2 - 36x - 5x + 180 = 0
x(x - 36) -5(x - 36) = 0
(x - 36)(x - 5) = 0
So, either
x - 36 = 0
x = 36
Or
x - 5 = 0
x = 5
But, the father’s age never be 5 years
Therefore, when x = 36 then
45 - x = 45 - 36 = 9
Hence, man’s present age is36 years and his son’s age is 9 years.
APPEARS IN
RELATED QUESTIONS
The perimeter of a rectangular field is 82 m and its area is 400 m2. Find the breadth of the rectangle.
In a class test, the sum of the marks obtained by P in Mathematics and science is 28. Had he got 3 marks more in mathematics and 4 marks less in Science. The product of his marks would have been 180. Find his marks in two subjects.
Solve the following quadratic equations by factorization:
`(x-3)/(x+3 )+(x+3)/(x-3)=2 1/2`
Solve for x: `3x^2-2sqrt3x+2=0`
One of the roots of equation 5m2 + 2m + k = 0 is `(-7)/5` Complete the following activity to find the value of 'k'.
Solve the following equation by factorization
`a/(ax - 1) + b/(bx - 1) = a + b, a + b ≠ 0, ab ≠ 0`
In a certain positive fraction, the denominator is greater than the numerator by 3. If 1 is subtracted from both the numerator and denominator, the fraction is decreased by `(1)/(14)`. Find the fraction.
A rectangular garden 10 m by 16 m is to be surrounded by a concrete walk of uniform width. Given that the area of the walk is 120 square metres, assuming the width of the walk to be x, form an equation in x and solve it to find the value of x.
A wire ; 112 cm long is bent to form a right angled triangle. If the hypotenuse is 50 cm long, find the area of the triangle.
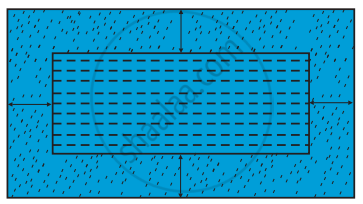
In the centre of a rectangular lawn of dimensions 50 m × 40 m, a rectangular pond has to be constructed so that the area of the grass surrounding the pond would be 1184 m2 [see figure]. Find the length and breadth of the pond.