Question

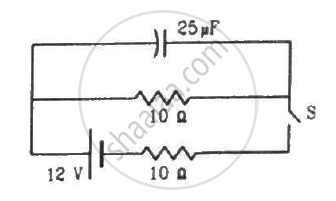
The switch S shown in figure is kept closed for a long time and is then opened at t = 0. Find the current in the middle 10 Ω resistor at t = 1 ms.

Answer 1

Initially, the switch S was closed; so, the capacitor was getting charged. Also, the two resistors are connected in parallel. The equivalent resistance of the circuit,

\[R = \frac{1}{\frac{1}{10} + \frac{1}{10}} = 5 \Omega\]

Initially, the switch was closed and the capacitor was getting charged. So, the two resistances were in parallel connection. Hence, their effective resistance will be 5 Ω.
Potential difference across the 10 Ω resistance,

\[V = \frac{12}{5} \times 10 = 24 V\]

When the switch is opened, the decay of charge through the capacitor,

\[Q = Q_0 e^{- \frac{t}{RC}} = V \times C e^{- \frac{t}{RC}} \]

\[\frac{t}{RC} = \frac{1 \times {10}^{- 3}}{10 \times 25 \times {10}^{- 6}} = \frac{1000}{250} = 4\]

\[ \Rightarrow Q = 24 \times 25 \times {10}^{- 6} \times e^{- 4} \]

\[ = 24 \times 25 \times {10}^{- 6} \times 0 . 0183\]

\[ = 10 . 9 \times {10}^{- 6} C\]

Current in the 10 Ω resistor,

\[i = \frac{Q}{t} = \frac{10 . 9 \times {10}^{- 6} C}{1 \times {10}^{- 3} \sec} = 11 mA\]