Advertisements
Advertisements
Question
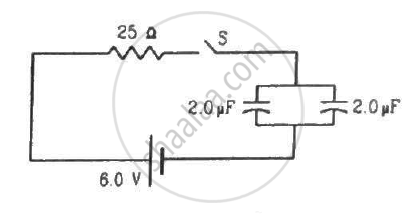
Find the charge on each of the capacitors 0.20 ms after the switch S is closed in the figure.
Solution
The equivalent capacitance of the circuit,
\[C_{eqv} = C_1 + C_2 = 2 + 2 = 4 \mu F\]
The growth of charge through the capacitor,
q = q0(1 − e−t/RC)
\[q_0 = CV = 4 \times {10}^{- 6} \times 6 = 24 \times {10}^{- 6} C\]
\[\frac{t}{RC} = \frac{0 . 20 \times {10}^{- 3}}{25 \times 4 \times {10}^{- 6}} = 2\]
⇒ q = 24 × 10−6 (1 − e−2)
= 18.4 × 10−6 C
This is the total charge on both capacitors. As the capacitors are in parallel, the total charge will be shared between them. Also, both the capacitors are of same capacitance; so, they will share equal amount of charge.
∴ Charge on each capacitor \[= \frac{18 . 4}{2} \mu C = 9 . 2 \mu C\]
APPEARS IN
RELATED QUESTIONS
A 12 pF capacitor is connected to a 50 V battery. How much electrostatic energy is stored in the capacitor?
In the following arrangement of capacitors, the energy stored in the 6 µF capacitor is E. Find the value of the following :
(i) Energy stored in 12 µF capacitor.
(ii) Energy stored in 3 µF capacitor.
(iii) Total energy drawn from the battery.
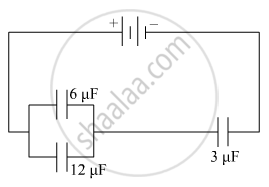
Find the ratio of energy stored in the two configurations if they are both connected to the same source.
A capacitor of capacitance 500 μF is connected to a battery through a 10 kΩ resistor. The charge stored in the capacitor in the first 5 s is larger than the charge stored in the next.
(a) 5 s
(b) 50 s
(c) 500 s
(d) 500 s
A capacitor C1 of capacitance 1 μF and a capacitor C2 of capacitance 2 μF are separately charged by a common battery for a long time. The two capacitors are then separately discharged through equal resistors. Both the discharge circuits are connected at t = 0.
(a) The current in each of the two discharging circuits is zero at t = 0.
(b) The currents in the two discharging circuits at t = 0 are equal but not zero.
(c) The currents in the two discharging circuits at t = 0 are unequal.
(d) C1 loses 50% of its initial charge sooner than C2 loses 50% of its initial charge.
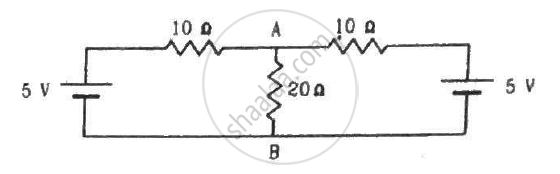
(a) Find the current in the 20 Ω resistor shown in the figure. (b) If a capacitor of capacitance 4 μF is joined between the points A and B, what would be the electrostatic energy stored in it in steady state?
How many time constants will elapse before the current in a charging RC circuit drops to half of its initial value? Answer the same question for a discharging RC circuit.
A capacitance C charged to a potential difference V is discharged by connecting its plates through a resistance R. Find the heat dissipated in one time constant after the connections are made. Do this by calculating ∫ i2R dt and also by finding the decrease in the energy stored in the capacitor.
By evaluating ∫i2Rdt, show that when a capacitor is charged by connecting it to a battery through a resistor, the energy dissipated as heat equals the energy stored in the capacitor.
A capacitor with stored energy 4⋅0 J is connected with an identical capacitor with no electric field in between. Find the total energy stored in the two capacitors.
A capacitor of capacitance C is given a charge Q. At t = 0, it is connected to an ideal battery of emf ε through a resistance R. Find the charge on the capacitor at time t.
Choose the correct option:
Energy stored in a capacitor and dissipated during charging a capacitor bear a ratio.
If the p. d. across a capacitor is increased from 10 V to 30 V, then the energy stored with the capacitor ____________.
A parallel plate condenser is immersed in an oil of dielectric constant 2. The field between the plates is ______.
A parallel plate capacitor has a uniform electric field `overset(->)("E")` in the space between the plates. If the distance between the plates is ‘d’ and the area of each plate is ‘A’, the energy stored in the capacitor is ______
(ε0 = permittivity of free space)
A fully charged capacitor C with initial charge q0 is connected to a coil of self-inductance L at t = 0. The time at which the energy is stored equally between the electric and magnetic fields is ______.
Electrostatic energy of 4 x 10−4 J is stored in a charged 25 pF capacitor. Find the charge on the capacitor.
Derive an expression for energy stored in a capacitor.
