Advertisements
Advertisements
Question
A capacitance C charged to a potential difference V is discharged by connecting its plates through a resistance R. Find the heat dissipated in one time constant after the connections are made. Do this by calculating ∫ i2R dt and also by finding the decrease in the energy stored in the capacitor.
Solution 1
Let Q0 be the initial charge on the capacitor. Then,
Q0 = CV
The charge on the capacitor at time t after the connections are made,
\[Q = Q_0 e^{- \frac{t}{RC}}\]
\[i = \frac{dQ}{dt} = - \left( \frac{Q_0}{RC} \right) e^{- \frac{t}{RC}}\]
Heat dissipated during time t1 to t2,
\[U = \int_{t_1}^{t_2} i^2 Rdt\]
\[ = \frac{{Q_0}^2}{2C}\left( e^{- \frac{2 t_1}{RC}} - e^{- \frac{2 t_2}{RC}} \right)\]
Time constant = RC
Putting t1 = 0 and t2 = RC, we get:-
\[U = \frac{{Q_0}^2}{2C}\left( e^{- 0} - e^{- 2} \right)\]
\[ \because Q_0 = CV, \]
\[ U = \frac{CV^2}{2}\left( 1 - \frac{1}{e^2} \right)\]
Solution 2
Heat dissipated at any time = Energy stored at time 0 − Energy stored at time t
\[\Rightarrow U = \frac{1}{2}C V^2 - \frac{1}{2}C V^2 e^{- \frac{2t}{RC}} \]
\[ \because t = RC, \]
\[ U = \frac{1}{2}C V^2 - \frac{1}{2}C V^2 e^{- 2} \]
\[ \Rightarrow U = \frac{1}{2}C V^2 \left( 1 - \frac{1}{e^2} \right)\]
APPEARS IN
RELATED QUESTIONS
Explain what would happen if the capacitor given in previous question a 3 mm thick mica sheet (of dielectric constant = 6) were inserted between the plates,
- While the voltage supply remained connected.
- After the supply was disconnected.
The energy density in the electric field created by a point charge falls off with the distance from the point charge as
A capacitor of capacitance 500 μF is connected to a battery through a 10 kΩ resistor. The charge stored in the capacitor in the first 5 s is larger than the charge stored in the next.
(a) 5 s
(b) 50 s
(c) 500 s
(d) 500 s
The plates of a capacitor of capacitance 10 μF, charged to 60 μC, are joined together by a wire of resistance 10 Ω at t = 0. Find the charge on the capacitor in the circuit at (a) t = 0 (b) t = 30 μs (c) t = 120 μs and (d) t = 1.0 ms.
Two capacitors of capacitances 4⋅0 µF and 6⋅0 µF are connected in series with a battery of 20 V. Find the energy supplied by the battery.
By evaluating ∫i2Rdt, show that when a capacitor is charged by connecting it to a battery through a resistor, the energy dissipated as heat equals the energy stored in the capacitor.
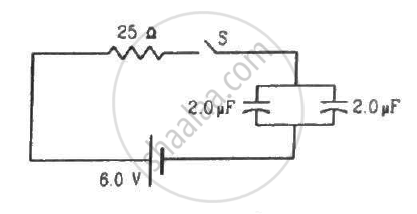
Find the charge on each of the capacitors 0.20 ms after the switch S is closed in the figure.
A capacitor of capacitance 100 μF is connected across a battery of emf 6 V through a resistance of 20 kΩ for 4 s. The battery is then replaced by a thick wire. What will be the charge on the capacitor 4 s after the battery is disconnected?
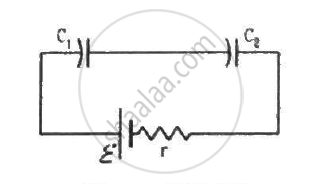
Consider the situation shown in figure. The switch is closed at t = 0 when the capacitors are uncharged. Find the charge on the capacitor C1 as a function of time t.
A metal sphere of radius R is charged to a potential V.
- Find the electrostatic energy stored in the electric field within a concentric sphere of radius 2 R.
- Show that the electrostatic field energy stored outside the sphere of radius 2 R equals that stored within it.
A large conducting plane has a surface charge density `1.0 xx 10^-4 "Cm"^-2` . Find the electrostatic energy stored in a cubical volume of edge 1⋅0 cm in front of the plane.
If the p. d. across a capacitor is increased from 10 V to 30 V, then the energy stored with the capacitor ____________.
A capacitor is charged by a battery and energy stored is 'U'. Now the battery is removed and the distance between plates is increased to four times. The energy stored becomes ______.
A 2µF capacitor is charge to 100 volt and then its plate are connected by a conducting wire. The heat produced is:-
What fraction of the energy drawn from the charging battery is stored in a capacitor?
Do free electrons travel to region of higher potential or lower potential?
A fully charged capacitor C with initial charge q0 is connected to a coil of self-inductance L at t = 0. The time at which the energy is stored equally between the electric and magnetic fields is ______.
A parallel plate capacitor (A) of capacitance C is charged by a battery to voltage V. The battery is disconnected and an uncharged capacitor (B) of capacitance 2C is connected across A. Find the ratio of total electrostatic energy stored in A and B finally and that stored in A initially.
