Advertisements
Advertisements
Question
Explain what would happen if the capacitor given in previous question a 3 mm thick mica sheet (of dielectric constant = 6) were inserted between the plates,
- While the voltage supply remained connected.
- After the supply was disconnected.
Solution
- Dielectric constant of the mica sheet, k = 6
Initial capacitance, C = 1.771 × 10−11 F
New Capacitance, C' = kC
= 6 × 1.771 × 10−11
= 106 pF
Supply voltage, V = 100 V
New Capacitance, q' = C'V
= 6 × 1.771 × 10−9
= 1.06 × 10−8 C
Potential across the plates remains 100 V. - Dielectric constant, k = 6
Initial capacitance, C = 1.771 × 10−11 F
New Capacitance, C' = kC
= 6 × 1.771 × 10−11
= 106 pF
If the supply voltage is removed, then there will be no effect on the amount of charge in the plates.
Charge = 1.771 × 10−9 C
Potential across the plates comes from,
∴ `"V'" = "q"/"C'"`
= `(1.771 xx 10^-9)/(106 xx 10^-12)`
= 16.7 V
APPEARS IN
RELATED QUESTIONS
Obtain the expression for the energy stored per unit volume in a charged parallel plate capacitor.
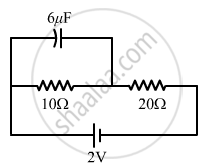
Find the charge on the capacitor as shown in the circuit.
A 100 μF capacitor is joined to a 24 V battery through a 1.0 MΩ resistor. Plot qualitative graphs (a) between current and time for the first 10 minutes and (b) between charge and time for the same period.
How many time constants will elapse before the energy stored in the capacitor reaches half of its equilibrium value in a charging RC circuit?
Answer the following question.
Obtain the expression for the energy stored in a capacitor connected across a dc battery. Hence define energy density of the capacitor
Choose the correct option:
Energy stored in a capacitor and dissipated during charging a capacitor bear a ratio.
A parallel plate condenser is immersed in an oil of dielectric constant 2. The field between the plates is ______.
A fully charged capacitor C with initial charge q0 is connected to a coil of self-inductance L at t = 0. The time at which the energy is stored equally between the electric and magnetic fields is ______.
A parallel plate capacitor (A) of capacitance C is charged by a battery to voltage V. The battery is disconnected and an uncharged capacitor (B) of capacitance 2C is connected across A. Find the ratio of total electrostatic energy stored in A and B finally and that stored in A initially.
Electrostatic energy of 4 x 10−4 J is stored in a charged 25 pF capacitor. Find the charge on the capacitor.
