Advertisements
Advertisements
Question
How many time constants will elapse before the current in a charging RC circuit drops to half of its initial value? Answer the same question for a discharging RC circuit.
Solution
The growth of charge across a capacitor,
\[q = Q\left( 1 - e^{- \frac{t}{RC}} \right)\]
\[q = \frac{Q}{2}\]
\[ \Rightarrow \frac{Q}{2} = Q \left( 1 - e^{- \frac{t}{RC}} \right)\]
\[ \Rightarrow \frac{1}{2} = \left( 1 - e^{- \frac{t}{RC}} \right)\]
\[ \Rightarrow e^{- \frac{t}{RC}} = \frac{1}{2}\]
\[ \Rightarrow \frac{t}{RC} = \ln 2 \]
Let t = nRC
\[ \Rightarrow \frac{nRC}{RC} = 0 . 69\]
\[ \Rightarrow n = 0 . 69\]
The decay of charge across a capacitor,
\[q = Q e^{- \frac{t}{RC}} \]
\[q = \frac{Q}{2}\]
\[ \Rightarrow \frac{Q}{2} = Q e^{- \frac{t}{RC}} \]
\[ \Rightarrow \frac{1}{2} = e^{- \frac{t}{RC}} \]
Let t = nRC
\[ \Rightarrow \frac{nRC}{RC} = \ln 2\]
\[ \Rightarrow n = 0 . 69\]
APPEARS IN
RELATED QUESTIONS
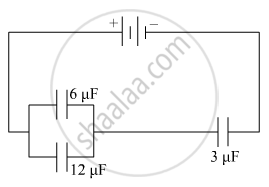
In the following arrangement of capacitors, the energy stored in the 6 µF capacitor is E. Find the value of the following :
(i) Energy stored in 12 µF capacitor.
(ii) Energy stored in 3 µF capacitor.
(iii) Total energy drawn from the battery.
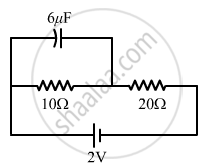
Find the charge on the capacitor as shown in the circuit.
A capacitor C1 of capacitance 1 μF and a capacitor C2 of capacitance 2 μF are separately charged by a common battery for a long time. The two capacitors are then separately discharged through equal resistors. Both the discharge circuits are connected at t = 0.
(a) The current in each of the two discharging circuits is zero at t = 0.
(b) The currents in the two discharging circuits at t = 0 are equal but not zero.
(c) The currents in the two discharging circuits at t = 0 are unequal.
(d) C1 loses 50% of its initial charge sooner than C2 loses 50% of its initial charge.
The plates of a capacitor of capacitance 10 μF, charged to 60 μC, are joined together by a wire of resistance 10 Ω at t = 0. Find the charge on the capacitor in the circuit at (a) t = 0 (b) t = 30 μs (c) t = 120 μs and (d) t = 1.0 ms.
A 100 μF capacitor is joined to a 24 V battery through a 1.0 MΩ resistor. Plot qualitative graphs (a) between current and time for the first 10 minutes and (b) between charge and time for the same period.
How many time constants will elapse before the energy stored in the capacitor reaches half of its equilibrium value in a charging RC circuit?
Two capacitors of capacitances 4⋅0 µF and 6⋅0 µF are connected in series with a battery of 20 V. Find the energy supplied by the battery.
A capacitor of capacitance 12.0 μF is connected to a battery of emf 6.00 V and internal resistance 1.00 Ω through resistanceless leads. 12.0 μs after the connections are made, what will be (a) the current in the circuit (b) the power delivered by the battery (c) the power dissipated in heat and (d) the rate at which the energy stored in the capacitor is increasing?
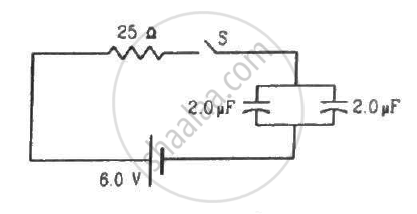
Find the charge on each of the capacitors 0.20 ms after the switch S is closed in the figure.
A capacitor with stored energy 4⋅0 J is connected with an identical capacitor with no electric field in between. Find the total energy stored in the two capacitors.
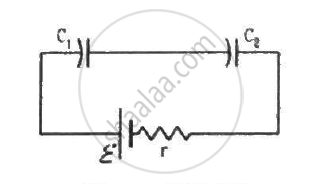
Consider the situation shown in figure. The switch is closed at t = 0 when the capacitors are uncharged. Find the charge on the capacitor C1 as a function of time t.
A capacitor of capacitance C is given a charge Q. At t = 0, it is connected to an uncharged capacitor of equal capacitance through a resistance R. Find the charge on the second capacitor as a function of time.
A capacitor is a device that stores ____________.
An air-filled parallel plate capacitor has a uniform electric field `overset(->)("E")` in the space between the plates. If the distance between the plates is 'd' and the area of each plate is 'A', the energy stored in the capacitor is ______
(∈0 = permittivity of free space)
A parallel plate capacitor has a uniform electric field `overset(->)("E")` in the space between the plates. If the distance between the plates is ‘d’ and the area of each plate is ‘A’, the energy stored in the capacitor is ______
(ε0 = permittivity of free space)
A fully charged capacitor C with initial charge q0 is connected to a coil of self-inductance L at t = 0. The time at which the energy is stored equally between the electric and magnetic fields is ______.
A parallel plate capacitor (A) of capacitance C is charged by a battery to voltage V. The battery is disconnected and an uncharged capacitor (B) of capacitance 2C is connected across A. Find the ratio of total electrostatic energy stored in A and B finally and that stored in A initially.
Electrostatic energy of 4 x 10−4 J is stored in a charged 25 pF capacitor. Find the charge on the capacitor.
In a capacitor of capacitance 20 µF, the distance between the plates is 2 mm. If a dielectric slab of width 1 mm and dielectric constant 2 is inserted between the plates, what is the new capacitance?
