Advertisements
Advertisements
Question
In the following arrangement of capacitors, the energy stored in the 6 µF capacitor is E. Find the value of the following :
(i) Energy stored in 12 µF capacitor.
(ii) Energy stored in 3 µF capacitor.
(iii) Total energy drawn from the battery.
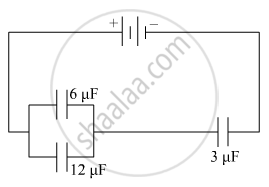
Solution
(i) Given that energy of the 6 µF capacitor is E.
Let V be the potential difference along the capacitor of capacitance 6 µF.
\[\text { Since } \frac{1}{2}C V^2 = E\]
\[ \therefore \frac{1}{2} \times 6 \times {10}^{- 6} \times V^2 = E\]
\[ \Rightarrow V^2 = \frac{E}{3} \times {10}^6 . . . (1)\]
Since potential is same for parallel connection, the potetial through 12 µF capacitor is also V. Hence, energy of 12 µF capacitor is
\[E_{12} = \frac{1}{2} \times 12 \times {10}^{- 6} \times V^2 = \frac{1}{2} \times 12 \times {10}^{- 6} \times \frac{E}{3} \times {10}^6 = 2E\]
(ii) Since charge remains constant in series, the charge on 6 µF and 12 µF capacitors combined will be equal to the charge on 3 µF capacitor. Using the formula, Q = CV, we can write
\[(6 + 12) \times {10}^{- 6} \times V = 3 \times {10}^{- 6} \times V'\]
\[\text { Using (1) and squaring both sides, we get }\]
\[V '^2 = 12E \times {10}^6 \]
\[ \therefore E_3 = \frac{1}{2} \times 3 \times {10}^{- 6} \times 12E \times {10}^6 = 18E\]
(iii) Total energy drawn from battery is
APPEARS IN
RELATED QUESTIONS
Find the ratio of energy stored in the two configurations if they are both connected to the same source.
The energy density in the electric field created by a point charge falls off with the distance from the point charge as
Find the charge on the capacitor shown in the figure.
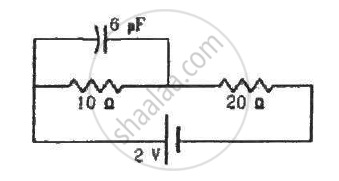
(a) Find the current in the 20 Ω resistor shown in the figure. (b) If a capacitor of capacitance 4 μF is joined between the points A and B, what would be the electrostatic energy stored in it in steady state?
How many time constants will elapse before the charge on a capacitors falls to 0.1% of its maximum value in a discharging RC circuit?
A capacitor of capacitance C is given a charge Q. At t = 0, it is connected to an uncharged capacitor of equal capacitance through a resistance R. Find the charge on the second capacitor as a function of time.
A capacitor of capacitance C is given a charge Q. At t = 0, it is connected to an ideal battery of emf ε through a resistance R. Find the charge on the capacitor at time t.
A point charge Q is placed at the origin. Find the electrostatic energy stored outside the sphere of radius R centred at the origin.
Answer the following question.
Obtain the expression for the energy stored in a capacitor connected across a dc battery. Hence define energy density of the capacitor
Prove that, if an insulated, uncharged conductor is placed near a charged conductor and no other conductors are present, the uncharged body must be intermediate in potential between that of the charged body and that of infinity.
