Advertisements
Advertisements
Question
To ensure almost 100 per cent transmissivity, photographic lenses are often coated with a thin layer of dielectric material. The refractive index of this material is intermediated between that of air and glass (which makes the optical element of the lens). A typically used dielectric film is MgF2 (n = 1.38). What should the thickness of the film be so that at the center of the visible spectrum (5500 Å) there is maximum transmission.
Advertisements
Solution
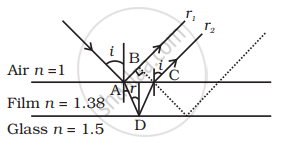
Consider a ray incident at an angle i. A part of this ray is reflected from the air-film interface and a part is refracted inside. This is partly reflected at the film-glass interface and a part transmitted. A part of the reflected ray is reflected at the film-air interface and a part is transmitted as r2 parallel to r1. Of course, successive reflections and transmissions will keep on decreasing the amplitude of the wave. Hence rays r1 and r2 shall dominate the behaviour. If the incident light is to be transmitted through the lens, r1 and r2 should interfere destructively. Both the reflections at A and D are from lower to higher refractive index and hence there is no phase change on reflection. The optical path difference between r2 and r1 is n (AD + CD) – AB.
If d is the thickness of the film, then
`AD = CD = d/cos r`
`AB = AC sin i`
`(AC)/2` = d tan r
∴ `AC = 2d tan r`
Hence, `AB = 2d tanr sini`
Thus the optical path difference is
`2n d/cos r - 2d tan r sin i`
= `2. sin i/sin r d/cos r - 2d sinr/cos r sin i`
= `2d sin [(1 - sin^2r)/(sinr cos r)]`
= `2 nd cos r`
For these waves to interfere destructively this must be `λ/2`.
⇒ `2nd cos r = λ/2`
or `nd cos r = λ/4`
For a camera lens, the sources are in the vertical plane and hence `i ≃ r ≃ 0`
∴ `nd ≃ λ/4`
⇒ `d = (5500 Å)/(1.38 xx 4) ≃ 1000 Å`
APPEARS IN
RELATED QUESTIONS
Show, using a simple polaroid, that light waves are transverse in nature. Intensity of light coming out of a polaroid does not change irrespective of the orientation of the pass axis of the polaroid. Explain why.
How does one demonstrate, using a suitable diagram, that unpolarised light when passed through a Polaroid gets polarised?
A beam of unpolarised light is incident on a glass-air interface. Show, using a suitable ray diagram, that light reflected from the interface is totally polarised, when μ = tan iB, where μ is the refractive index of glass with respect to air and iB is the Brewster's angle.
Two polaroids P1 and P2 are placed with their pass axes perpendicular to each other. Unpolarised light of intensity I0 is incident on P1. A third polaroid P3 is kept in between P1 and P2 such that its pass axis makes an angle of 60° with that of P1. Determine the intensity of light transmitted through P1, P2 and P3.
When a low flying aircraft passes overhead, we sometimes notice a slight shaking of the picture on our TV screen. Suggest a possible explanation.
A ray of light passes from a vacuum to a medium of refractive index (μ). The angle of
incidence is found to be twice the angle of refraction. The angle of incidence is _______.
A) `cos^(-1)(mu/2)`
B) cos−1(μ)
C) `2 cos^(-1) (mu/2)`
D) `2 sin^(-1) (mu/2)`
State two uses of Polaroid.
Show using a proper diagram how unpolarised light can be linearly polarised by reflection from a transparent glass surface.
With the help of an experiment, state how will you identify whether a given beam of light is polarised or unpolarized?
Green light is incident at the polarising angle on a certain transparent medium. The angle of refraction is 30° . Find
(i) polarising angle, and
(ii) refractive index of the medium.
A ray of light is incident on a transparent medium at a polarizing angle. What is the angle between the reflected ray and the refracted ray?
A ray of ordinary light is travelling in air. It is incident on air glass pair at a polarising angle of 56°. Find the angle of refraction in glass.
Discuss polarisation by selective absorption.
What is a analyser?
List the uses of polaroids.
An unpolarised light of intensity 32 Wm-2 passes through three Polaroids such that the axes of the first and the last Polaroids are at 90°. What is the angle between the axes of the first and middle Polaroids so that the emerging light has an intensity of only 3 Wm-2?
Consider a light beam incident from air to a glass slab at Brewster’s angle as shown in figure. A polaroid is placed in the path of the emergent ray at point P and rotated about an axis passing through the centre and perpendicular to the plane of the polaroid.
For the same objective, find the ratio of the least separation between two points to be distinguished by a microscope for light of 5000 Å and electrons accelerated through 100 V used as the illuminating substance.
Figure shown a two slit arrangement with a source which emits unpolarised light. P is a polariser with axis whose direction is not given. If I0 is the intensity of the principal maxima when no polariser is present, calculate in the present case, the intensity of the principal maxima as well as of the first minima.
