Advertisements
Advertisements
Question
Two circles of radii 5 cm and 3 cm intersect at two points and the distance between their centres is 4 cm. Find the length of the common chord.
Solution
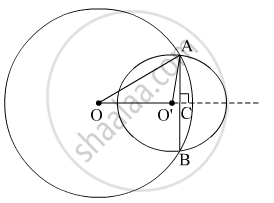
Let the radius of the circle centered at O and O' be 5 cm and 3 cm respectively.
OA = OB = 5 cm
O'A = O'B = 3 cm
OO' will be the perpendicular bisector of chord AB.
∴ AC = CB
It is given that, OO' = 4 cm
Let OC be x. Therefore, O'C will be x − 4
In ΔOAC,
OA2 = AC2 + OC2
⇒ 52 = AC2 + x2
⇒ 25 − x2 = AC2 ... (1)
In ΔO'AC,
O'A2 = AC2 + O'C2
⇒ 32 = AC2 + (x − 4)2
⇒ 9 = AC2 + x2 + 16 − 8x
⇒ AC2 = − x2 − 7 + 8x ... (2)
From equations (1) and (2), we obtain
25 − x2 = − x2 − 7 + 8x
8x = 32
x = 4
Therefore, the common chord will pass through the centre of the smaller circle i.e., O' and hence, it will be the diameter of the smaller circle.

Length of the common chord AB = 2 O'A = (2 × 3) cm = 6 cm.
APPEARS IN
RELATED QUESTIONS
If two equal chords of a circle intersect within the circle, prove that the segments of one chord are equal to corresponding segments of the other chord.
If a line intersects two concentric circles (circles with the same centre) with centre O at A, B, C, and D, prove that AB = CD (see given figure).

true or false
A circle has only finite number of equal chords.
An equilateral triangle of side 9cm is inscribed in a circle. Find the radius of the circle.
Two chords AB and CD of lengths 5 cm and 11 cm respectively of a circle are parallel to each other and are opposite side of its center. If the distance between AB and CD is 6 cm. Find the radius of the circle.
If two diameters of a circle intersect each other at right angles, then quadrilateral formed by joining their end points is a
Angle formed in minor segment of a circle is
In a circle with centre O, AB and CD are two diameters perpendicular to each other. The length of chord AC is
Two equal circles of radius r intersect such that each passes through the centre of the other. The length of the common chord of the circle is
AB and AC are two chords of a circle of radius r such that AB = 2AC. If p and q are the distances of AB and AC from the centre, prove that 4q2 = p2 + 3r2.
