Advertisements
Advertisements
Question
Two exactly similar electric lamps are arranged (i) in parallel, and (ii) in series. If the parallel and series combination of lamps are connected to 220 V supply line one by one, what will be the ratio of electric power consumed by them?
Solution
Let R be the resistance of the lamp and V be the potential difference applied.
In a series connection:
Net resistance of the circuit, R1 = R + R = 2R
Power drawn, P1 = V2/R1 = V2/2R
In a parallel connection:
Net resistance of the circuit, R2 will be:
`1/R_2=1/R+1/R=2/R` or `R_2=R/2`
Power drawn, P2 = V2/R2 = 2V2/R
Therefore, P2:P1 = 4:1
APPEARS IN
RELATED QUESTIONS
A 4 Ω coil and a 2 Ω coil are connected in parallel. What is their combined resistance? A total current of 3 A passes through the coils. What current passes through the 2 Ω coil?
How will you connect three resistors of resistances 2 Ω, 3 Ω, and 6 Ω to obtain a total resistance of 4 Ω, and 1 Ω?
State how are the two resistors joined with a battery when equivalent resistance is less than either of the two resistances.
A uniform wire with a resistance of 27 Ω is divided into three equal pieces and then they are joined in parallel. Find the equivalent resistance of the parallel combination.
A battery of e.m.f. 15 V and internal resistance 2 `Omega` is connected to tvvo resistors of 4 ohm and 6 ohm joined.
(i) In series,
(ii) In para 1 lel. Find in each case the electrica I energy spent per minute in 6 ohm resistor.
Solve the following question:
In an electric circuit, two resistors of 12 0 each are joined in parallel to a 6 V battery. Find the current drawn from the battery.
How does the resistance of a metallic wire depend on the length of wire?
A given wire is stretched to double its length. How will its resistance change?
Calculate equivalent resistance in the following cases:
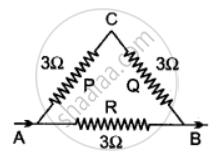
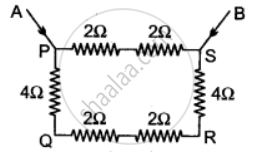
Two resistors when connected in parallel give the resultant resistance of 2 ohms, but when connected in series the effective resistance becomes 9 ohms. Calculate the value of each resistance.
