Advertisements
Advertisements
Question
Two spheres A and B of radius a and b respectively are at the same potential. Find the ratio of the surface charge densities of A and B.
Solution
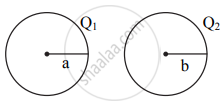
Since the electric potential is the same, `1/(4piepsilon_0) "Q"_1/"a" = 1/(4piepsilon_0) "Q"_2/"b"`
∴ `"Q"_1/"Q"_2 = "a"/"b"`
But σ1 = `"Q"_1/(4pi"a"^2)` and σ2 = `"Q"_2/(4pi"b"^2)`
∴ `σ_1/σ_2 = "Q"_1/"Q"_2 xx "b"^2/"a"^2 = "a"/"b" xx "b"^2/"a"^2 = "b"/"a"`
The ratio of the surface charge densities of A and B is b : a.
RELATED QUESTIONS
The safest way to protect yourself from lightning is to be inside a car. Justify.
What happens to the energy stored in a capacitor, if the plates of a charged capacitor are drawn apart, the battery remaining connected?
The capacity of the conductor does not depend upon ______
Two parallel conductors carrying unequal currents in the same direction ______.
The surface charge density of an irregular shaped conductor is ____________.
The surface density of charge on the surface of a charged conductor in the air is 0.885 `(muC)/m^2`. The outward force per unit area of charged conductor is ______
`(ε_0 = 8.85 xx 10^-12 C^2/(N - m^2))`
