Question

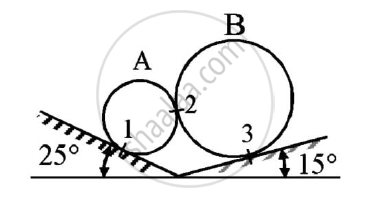
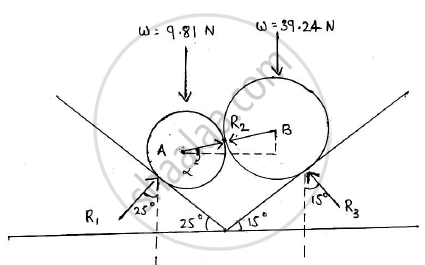
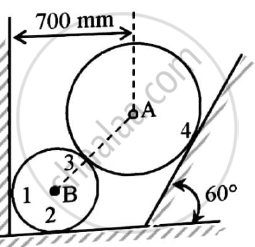
Two spheres A and B of weight 1000N and 750N respectively are kept as shown in the figure..Determine reaction at all contact points 1,2,3 and 4. Radius of A is 400 mm and radius of B is 300 mm

Given  : Two spheres are in equilibrium
W₁=1000 N
W₂=750 N
r_A=400 mm
r_B=300 mm 
To find : Reaction forces at contact points 1,2,3 and 4

Answer 1

BC = BP = 300mm = 0.3m
AP = 400 mm = 0.4 m
AB = AP + BP
    = 0.7m
CO = BC + BO
0.7 = 0.3 + BO
BO = 0.4m

In △AOB
`cos α = (BO)/(AB) = (0.4)/(0.7)`
α = cos^-1(0.5714) 
α = 55.1501^o 

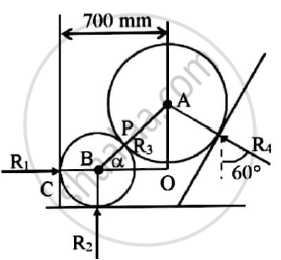
Forces R₃,R₄ and 1000N are under equilibrium at point A 

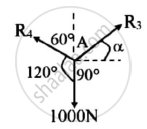
Applying Lami’s theorem
`(R3)/(sin120) = 1000/(sin (150−alpha)) = (R4)/(sin (90+alpha))`

`(R3)/(sin120) = 1000/(sin (150−55.1501)) = (R4)/(sin(90+55.1501))`
Solving the equations
R₃ = 869.1373 N
R₄ = 573.4819 N

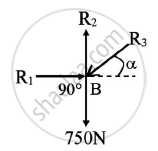
Forces R₁,R₂,R₃ and 750N are under equilibrium at B
Applying conditions of equilibrium

ΣF_Y=0 
-R₃sin α-750+R2=0 
R₂=869.1373 sin55.1501+750  
R₂=1463.2591 N (Acting upwards) 
Applying conditions of equilibrium

ΣF_X=0
R₁-R₃cosα=0 
R₁=869.1373cos55.1501  

R₁=496.65 N(Acting towards right)

Sr.no.	Point	Force
1.	R1	496.65 N(Towards right)
2.	R2	1463.2591 N(Towards up)
3.	R3	869.1373 N(55.1501o in first quadrant)
4.	R4	573.4819 N(30o in second quadrant)