Advertisements
Advertisements
Question
Use the mirror equation to show a convex mirror always produces a virtual image independent of the location of the object ?
Solution
A convex mirror
f > 0; u < 0 (always)
Case I |u| > |f|
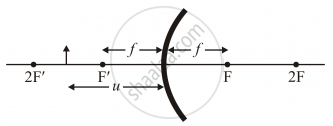
We know,
`v =(fu)/(u-f)`
`fu <0 and f-u<0`
`=> v>0 ` virtual image
Case `2|u|<|f|`
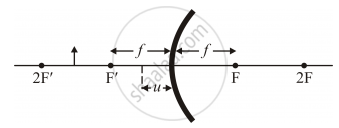
`v=(fu)/(u-f) fu<0`
`=> u> 0 u-f<0`
Hence, at all the positions convex mirror will form a virtual image.
APPEARS IN
RELATED QUESTIONS
Use the mirror equation to show that a convex mirror always produces a virtual image independent of the location of the object.
Use the mirror equation to deduce that an object placed between the pole and focus of a concave mirror produces a virtual and enlarged image.
Can a plane mirror ever form a real image?
The rays of different colours fail to converge at a point after going through a converging lens. This defect is called
Which of the following (referred to a spherical mirror) do (does) not depend on whether the rays are paraxial or not?
(a) Pole
(b) Focus
(c) Radius of curvature
(d) Principal axis
A light ray is incident at an angle of 45° with the normal to a √2 cm thick plate (μ = 2.0). Find the shift in the path of the light as it emerges out from the plate.
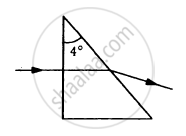
Find the angle of deviation suffered by the light ray shown in figure. The refractive index μ = 1.5 for the prism material.
Write any one use for each of the following mirrors :
(a) Convex
(b) Concave
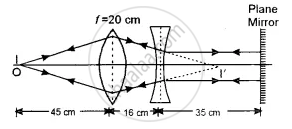
The figure below shows the positions of a point object O, two lenses, a plane mirror and the final image I which coincides with the object. The focal length of the convex lens is 20 cm. Calculate the focal length of the concave lens.
Car B overtakes car A at a relative speed of 40 ms-1. How fast will the image of car B appear to move in the mirror of focal length 10 cm fitted in car A, when car B is 1.9 m away from car A?
