Advertisements
Advertisements
Question
Use this law to obtain the expression for the magnetic field inside an air cored toroid of average radius 'r', having 'n' turns per unit length and carrying a steady current I.
Advertisements
Solution
A toroid is a hollow circular ring on which a large number of turns of a wire are closely wound. Consider an air-cored toroid (as shown above) with centre O.
Given:
r = Average radius of the toroid
I = Current through the solenoid
n = Number of turns per unit length
To determine the magnetic field inside the toroid, we consider three amperian loops (loop 1, loop 2 and loop 3) as show in the figure below.
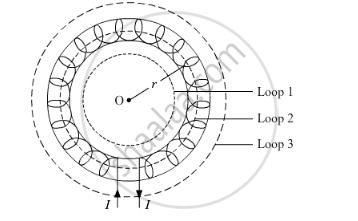
For loop 1:
According to Ampere's circuital law, we have
`ointvecB.vec(dl)=mu_0(`
Total current for loop 1 is zero because no current is passing through this loop.
So, for loop 1
`oint.vecB.vec(dl)=0`
For loop 3:
According to Ampere's circuital law, we have
`ointvecB.vec(dl)=mu_0(`
Total current for loop 3 is zero because net current coming out of this loop is equal to the net current going inside the loop.
For loop 2:
The total current flowing through the toroid is NI, where N is the total number of turns.
`ointvecB.vec(dl)=mu_0(NI)`
Now, `vecB `
`ointvecB.vec(dl)=Bointdl`
`=>ointvecB.vec(dl)=B(2pir)`
Comparing (i) and (ii), we get
B(2πr)=μ0NI
`=>B=(mu_0NI)/(2pir)`
Number of turns per unit length is given by
`n=N(2pir)`
∴B=μ0nI
This is the expression for magnetic field inside air-cored toroid.
APPEARS IN
RELATED QUESTIONS
Obtain the expression for mutual inductance of a pair of long coaxial solenoids each of length l and radii r1 and r2 (r2 >> r1). Total number of turns in the two solenoids are N1 and N2, respectively.
Define self-inductance of a coil.
A wire AB is carrying a steady current of 12 A and is lying on the table. Another wire CD carrying 5 A is held directly above AB at a height of 1 mm. Find the mass per unit length of the wire CD so that it remains suspended at its position when left free. Give the direction of the current flowing in CD with respect to that in AB. [Take the value of g = 10 ms−2]
A wire AB is carrying a steady current of 10 A and is lying on the table. Another wire CD carrying 6 A is held directly above AB at a height of 2 mm. Find the mass per unit length of the wire CD so that it remains suspended at its position when left free. Give the direction of the current flowing in CD with respect to that in AB. [Take the value of g = 10 ms−2]
In what respect is a toroid different from a solenoid?
Draw and compare the pattern of the magnetic field lines in the two cases ?
How is the magnetic field inside a given solenoid made strong?
A circular coil of one turn of radius 5.0 cm is rotated about a diameter with a constant angular speed of 80 revolutions per minute. A uniform magnetic field B = 0.010 T exists in a direction perpendicular to the axis of rotation. Suppose the ends of the coil are connected to a resistance of 100 Ω. Neglecting the resistance of the coil, find the heat produced in the circuit in one minute.
A long solenoid is fabricated by closely winding a wire of radius 0.5 mm over a cylindrical nonmagnetic frame so that the successive turns nearly touch each other. What would be the magnetic field B at the centre of the solenoid if it carries a current of 5 A?
A tightly-wound solenoid of radius a and length l has n turns per unit length. It carries an electric current i. Consider a length dx of the solenoid at a distance x from one end. This contains n dx turns and may be approximated as a circular current i n dx. (a) Write the magnetic field at the centre of the solenoid due to this circular current. Integrate this expression under proper limits to find the magnetic field at the centre of the solenoid. (b) verify that if l >> a, the field tends to B = µ0ni and if a >> l, the field tends to `B =(mu_0nil)/(2a)` . Interpret these results.
