∴ (A ∩ B)’ = A’ ∪ B’
Advertisements
Advertisements
Question
Verify (A ∩ B)’ = A’ ∪ B’ using Venn diagrams
Diagram
Solution
(i)
(ii)
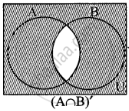
(iii)
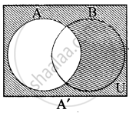
(iv)
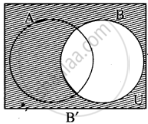
(v)
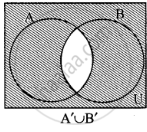
from (ii) and (v)
shaalaa.com
De Morgan’s Laws
Is there an error in this question or solution?
APPEARS IN
RELATED QUESTIONS
Using the adjacent Venn diagram, find the following set:
A – B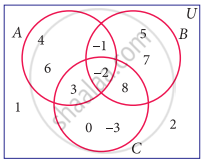
Using the adjacent Venn diagram, find the following set:
A’ ∩ B’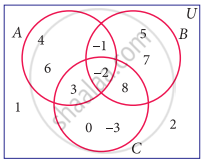
Using the adjacent Venn diagram, find the following set:
(B ∪ C)’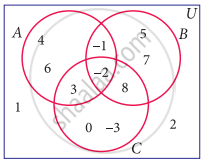
If K = {a, b, d, e, f}, L = {b, c, d, g} and M = {a, b, c, d, h} then find the following:
K ∪ (L ∩ M)
If K = {a, b, d, e, f}, L = {b, c, d, g} and M = {a, b, c, d, h} then find the following:
K ∩ (L ∪ M)
If A = {x : x ∈ Z, −2 < x ≤ 4}, B = {x : x ∈ W, x ≤ 5}, C = {− 4, −1, 0, 2, 3, 4} verify A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)
If A = {– 2, 0, 1, 3, 5}, B = {–1, 0, 2, 5, 6} and C = {–1, 2, 5, 6, 7}, then show that A – (B ∪ C) = (A – B) ∩ (A – C)
If A = `{y : y = ("a"+1)/2, "a" ∈ "W" and "a" ≤ 5}`, B = `{y : y = (2"n" – 1)/2, "n" ∈ "W" and "n" < 5}` and C = `{-1, −1/2, 1, 3/2, 2}` then show that A – (B ∪ C) = (A – B) ∩ (A – C)
Verify A – (B ∩ C) = (A – B) ∪ (A – C) using Venn diagrams
If U = {4, 7, 8, 10, 11, 12, 15, 16}, A = {7, 8, 11, 12} and B = {4, 8, 12, 15}, then verify De Morgan’s Laws for complementation
