Advertisements
Advertisements
Question
Verify the division algorithm i.e. Dividend = Divisor × Quotient + Remainder, in each of the following. Also, write the quotient and remainder.
| Dividend | Divisor |
| 4y3 + 8y + 8y2 + 7 | 2y2 − y + 1 |
Solution
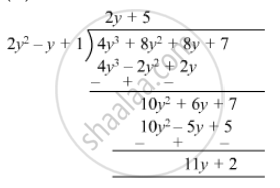
Quotient = 2y + 5
Remainder = 11y + 2
Divisor = 2y2 - y + 1
Divisor x Quotient + Remainder = (2y2 - y + 1) (2y + 5) + 11y + 2
= 4y3 +10y2 - 2y2 - 5y + 2y + 5 + 11y + 2
= 4y3 + 8y2 + 8y + 7
= Dividend
Thus,
Divisor x Quotient + Remainder = Dividend
Hence verified.
APPEARS IN
RELATED QUESTIONS
Write each of the following polynomials in the standard form. Also, write their degree.
x2 + 3 + 6x + 5x4
Simplify:\[\frac{16 m^3 y^2}{4 m^2 y}\]
Divide x4 − 2x3 + 2x2 + x + 4 by x2 + x + 1.
Using division of polynomials, state whether
z2 + 3 is a factor of z5 − 9z
Find whether the first polynomial is a factor of the second.
4y + 1, 8y2 − 2y + 1
Divide:
x2 − 5x + 6 by x − 3
Divide:
Divide: 8x − 10y + 6c by 2
Divide 24(x2yz + xy2z + xyz2) by 8xyz using both the methods.
Divide: 81(p4q2r3 + 2p3q3r2 – 5p2q2r2) by (3pqr)2
