Advertisements
Advertisements
Question
Verify Euler’s formula for the following three-dimensional figures:

Solution 1
(i)
Number of vertices = 6
Number of faces = 8
Number of edges = 12
Using Euler formula,
F + V – E = 2
8 + 6 – 12 = 2
2 = 2 Hence proved.
(ii)
Number of vertices = 9
Number of faces = 8
Number of edges = 15
Using, Euler’s formula,
F + V – E = 2
9 + 8 – 15 = 2
2 = 2 Hence proved.
(iii)
Number of vertices = 9
Number of faces = 5
Number of edges = 12
Using, Euler’s formula,
F + V – E = 2
9 + 5 – 12 = 2
2 = 2 Hence proved.
Solution 2
Euler's formula for three-dimensional polyhedra is given by: V − E + F = 2
- V = Number of vertices,
- E = Number of edges,
- F = Number of faces.
Shape 1: Double Pyramid (Octahedron)
- Vertices (V): 6 (4 vertices on the middle square + 2 vertices at the top and bottom tips).
- Edges (E): 12 (4 edges on the middle square + 4 edges connecting the top vertex to the square + 4 edges connecting the bottom vertex to the square).
- Faces (F): 8 (4 triangular faces on the top + 4 triangular faces on the bottom).
V − E + F
= 6 − 12 + 8 = 2
Shape 2: Square Pyramid
- Vertices (V): 5 (4 vertices on the square base + 1 vertex at the top tip).
- Edges (E): 8 (4 edges of the square base + 4 edges connecting the top vertex to each vertex of the square).
- Faces (F): 5 (4 triangular faces + 1 square base).
V − E + F
= 5 − 8 + 5 = 2
Shape 3: Triangular Prism
- Vertices (V): 6 (3 vertices on each triangular base).
- Edges (E): 9 (3 edges on each triangular base + 3 edges connecting the corresponding vertices of the two triangles).
- Faces (F): 5 (2 triangular bases + 3 rectangular faces connecting the sides of the triangles).
V − E + F
= 6 − 9 + 5 = 2
Verified.
APPEARS IN
RELATED QUESTIONS
Euler’s formula is true for all three-dimensional shapes.
Complete the table given below:
| S.No | Solid | Shape of Solid |
Number of faces F |
Number of Verticles V |
Number of edges E |
F + V | E + 2 |
| a. | Cuboid |  |
|||||
| b. | Triangular Pyramid |
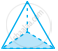 |
|||||
| c. | Square Pyramid |
 |
|||||
| d. | Rectangular Pyramid |
 |
|||||
| e. | Pentagonal Pyramid |
 |
|||||
| f. | Hexagonal Pyramid |
 |
|||||
| g. | Triangular Prism |
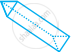 |
|||||
| h. | Square Prism |
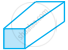 |
|||||
| i. | Cube |  |
|||||
| j. | Pentagonal Prism |
 |
|||||
| k. | Octagonal Prism |
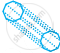 |
|||||
| l. | Heptagonal Prism |
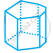 |
Look at the shapes given below and state which of these are polyhedra using Euler’s formula.
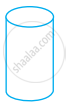
Look at the shapes given below and state which of these are polyhedra using Euler’s formula.
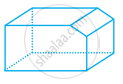
Look at the shapes given below and state which of these are polyhedra using Euler’s formula.
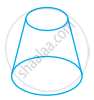
Look at the shapes given below and state which of these are polyhedra using Euler’s formula.
Look at the shapes given below and state which of these are polyhedra using Euler’s formula.
Look at the shapes given below and state which of these are polyhedra using Euler’s formula.

Using Euler’s formula, find the value of unknown x in the following table.
| Faces | 7 |
| Vertices | 10 |
| Edges | x |
Using Euler’s formula, find the value of unknown r in the following table.
| Faces | 8 |
| Vertices | 11 |
| Edges | r |
