Advertisements
Advertisements
Question
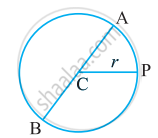
वृत का एक व्यास वह रेखाखंड है जो वृत पर स्थित दो बिन्दुओं को जोड़ता है और उसके केंद्र से होकर जाता है। वृत के व्यास (d) को उसकी त्रिज्या (r) के पदों में व्यक्त कीजिए।
Solution
व्यास = AB = AC + CB = r + r = 2r
d = 2r
APPEARS IN
RELATED QUESTIONS
बराबर लंबाई के रेखाखंडों से बनाए गए अंकों का पैटर्न को देखिए। आप रेखाखण्डों से बने हुए इस प्रकार के अंकों को इलेक्ट्रानिक घड़ियों या कैलकुलेटरों पर देख सकते हैं।
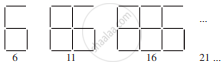(5n + 1)....
यदि बनाए गए अंकों की संख्या n ली जाए, तो उसके लिए आवश्यक रेखाखण्डों की n संख्या दर्शाने वाला बीजीय व्यंजक पैटर्न के दाईं ओर लिखा गया है।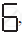 
के प्रकार के 5, 10, 100 अंकों को बनाने के लिए कितने रेखाखण्डों की आवश्यकता होगी?
बराबर लंबाई के रेखाखंडों से बनाए गए अंकों का पैटर्न को देखिए। आप रेखाखण्डों से बने हुए इस प्रकार के अंकों को इलेक्ट्रानिक घड़ियों या कैलकुलेटरों पर देख सकते हैं।
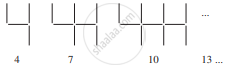(3n + 1)....
यदि बनाए गए अंकों की संख्या n ली जाए, तो उसके लिए आवश्यक रेखाखण्डों की n संख्या दर्शाने वाला बीजीय व्यंजक पैटर्न के दाईं ओर लिखा गया है। 
के प्रकार के 5, 10, 100 अंकों को बनाने के लिए कितने रेखाखण्डों की आवश्यकता होगी?
बराबर लंबाई के रेखाखंडों से बनाए गए अंकों का पैटर्न को देखिए। आप रेखाखण्डों से बने हुए इस प्रकार के अंकों को इलेक्ट्रानिक घड़ियों या कैलकुलेटरों पर देख सकते हैं।
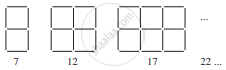(5n + 2)....
यदि बनाए गए अंकों की संख्या n ली जाए, तो उसके लिए आवश्यक रेखाखण्डों की n संख्या दर्शाने वाला बीजीय व्यंजक पैटर्न के दाईं ओर लिखा गया है। 
के प्रकार के 5, 10, 100 अंकों को बनाने के लिए कितने रेखाखण्डों की आवश्यकता होगी?
संख्या पैटर्नों की निम्नलिखित सारणी को पूरा करने के लिए, दिए हुए बीजीय व्यंजकों का प्रयोग कीजिए:
| क्रम संख्या |
व्यंजक |
पद | |||||||||
| पहला | दूसरा | तीसरा | चौथा | पाँचवाँ | ... | दसवाँ | ... | सौवाँ | ... | ||
| 1 | 2n - 1 | 1 | 3 | 5 | 7 | 9 | - | 19 | - | - | - |
| 2 | 3n + 2 | 5 | 8 | 11 | 14 | - | - | - | - | - | - |
| 3 | 4n + 1 | 5 | 9 | 13 | 17 | - | - | - | - | - | - |
| 4 | 7n + 20 | 27 | 34 | 41 | 48 | - | - | - | - | - | - |
| 5 | n2 + 1 | 2 | 5 | 10 | 17 | - | - | - | - | 10,001 | - |
एक समबाहु त्रिभुज की भुजा को l से दर्शाया जाता है। इस समबाहु त्रिभुज के परिमाप को l का प्रयोग करते हुए व्यक्त कीजिए।
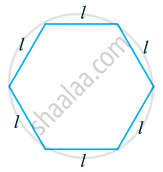
एक सम षड्भुज (Regular hexagon) की एक भुजा को l से व्यक्त किया गया है।l का प्रयोग करते हुए, इस षड्भुज के परिमाप को व्यक्त कीजिए।
(संकेत: एक समषड्भुज की सभी 6 भुजाएँ बराबर होती है और सभी कोण बराबर होते हैं)।
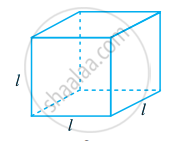
घन (Cube) एक त्रिवीमीय (three dimensional) आकृति होती है, जैसा कि में दिखाया गया है। इसके 6 फलक होते हैं और ये सभी सर्वसम (identical) वर्ग होते हैं। घन के एक किनारे की लंबाई l से दी जाती है। घन के किनारों की कुल लंबाई के लिए एक सूत्र ज्ञात कीजिए।
तीन संख्याओं 14, 27 और 13 के योग पर विचार कीजिए। हम यह योग दो प्रकार से प्राप्त कर सकते हैं:
- हम पहले 14 और 27 को जोड़कर 41 प्राप्त कर सकते हैं और फिर 41 में 13 जोड़कर कुल योग 54 प्राप्त कर सकते हैं।
- हम पहले 27 और 13 को जोड़कर 40 प्राप्त कर सकते हैं और फिर उसमें 14 जोड़कर कुल योग 54 प्राप्त कर सकते हैं। इस प्रकार (14+27)+13=14+(27+13) हुआ।
ऐसा किसी भी तीन संख्याओं के लिए किया जा सकता है। यह गुण संख्याओं के योग का साहचर्य (associative) गुण कहलाता है। इस गुण को जिसे हम पूर्ण संख्याओं के अध्याय में पढ़ चुके हैं, चर a, b और c का प्रयोग करते हुए, एक व्यापक रूप में व्यक्त कीजिए।
