Question

A pendulum bob of mass 50 g is suspended from the ceiling of an elevator. Find the tension in the string if the elevator (a) goes up with acceleration 1.2 m/s², (b) goes up with deceleration 1.2 m/s², (c) goes up with uniform velocity, (d) goes down with acceleration 1.2 m/s², (e) goes down with deceleration 1.2 m/s² and (f) goes down with uniform velocity.

Answer 1

(a) When the elevator goes up with acceleration 1.2 m/s²: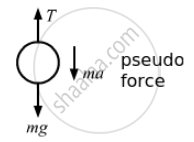

\[T = mg + ma\]
⇒ T = 0.05 (9.8 + 1.2) = 0.55 N
(b) Goes up with deceleration 1.2 m/s² :

\[T = mg + m\left( - a \right) = m\left( g - a \right)\]
⇒ T  = 0.05 (9.8 − 1.2) = 0.43 N

(c) Goes up with uniform velocity:

\[T = mg\]
⇒ T = 0.05 × 9.8 = 0.49 N

(d) Goes down with acceleration 1.2 m/s² :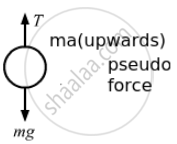

\[T + ma = mg\]
\[ \Rightarrow T = m\left( g - a \right)\]
⇒ T = 0.05 (9.8 − 1.2) = 0.43 N

(e) Goes down with deceleration 1.2 m/s² :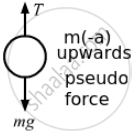

\[T + m\left( - a \right) = mg\]
\[ \Rightarrow T = m\left( g + a \right)\]
⇒ T = 0.05 (9.8 + 1.2) = 0.55 N

(f) Goes down with uniform velocity:

\[T = mg\]
⇒ T = 0.05 × 9.8 = 0.49 N