Advertisements
Advertisements
Question
Which of the following sequences are A.P.? If they are A.P. find the common difference.
Solution
The terms are given :
2, `5/2, 3, 7/2,......`
t2 − t1 = `5/2 - 2 = (5 - 4)/2 = 1/2`
t3 − t2 = `3 - 5/2 = (6 - 5)/2 = 1/2`
t4 − t3 = `7/2 - 3 = (7 - 6)/2 = 1/2`
∵ The difference between consecutive terms are constant.
∴ Given sequence is an A.P.
Common difference (d) = `1/2`
APPEARS IN
RELATED QUESTIONS
Find the sum of all three-digits natural numbers which are divisible by 13.
Find the sum of the following.
`(1 - 1/n) +(1 -2/n) + (1- 3/n) +` ......up to n terms.
In an AP. It is given that `s_5 + s_7 = 167 and s_10 = 235 ," then find the AP, where " S_n` denotes the sum of its first n terms.
In an AP, the first term is 2, the last term is 29 and the sum of all the terms is 155. Find the common difference.
The sum of the first 7 terms of an AP is 182. If its 4th and 17th terms are in the ratio 1:5, find the AP.
The 13th terms of an AP is 4 times its 3rd term. If its 5th term is 16, Find the sum of its first 10 terms.
The sum of first q terms of an AP is (63q – 3q2). If its pth term is –60, find the value of p. Also, find the 11th term of its AP.
Which of the following sequences are A.P.? If they are A.P. find the common difference.
–10, –6, –2, 2,...
Which of the following sequences are A.P. ? If they are A.P. find the common difference .
127, 132, 137,...
Write the correct number in the given boxes from the following A. P.
–3, –8, –13, –18,...
Here t3 =  , t2 =
, t2 =  , t4 =
, t4 = , t1 =
, t1 =  ,
,
t2 – t1 =  , t3 – t2 =
, t3 – t2 =  ∴ a =
∴ a =  , d =
, d = 
On 1st Jan 2016, Sanika decides to save Rs 10, Rs 11 on second day, Rs 12 on third day. If she decides to save like this, then on 31st Dec 2016 what would be her total saving?
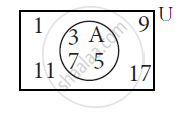
Observe the adjacent Venn diagram and write the complement of A.
Write a trinomial of degree 7.
Write the lower and the uppper class limit of 35 to 40
Solve : 5m² - 22m-15 = 0
Yogesh requires 3 days more than Vivek to do a work completely. If both
of them work together, the work can be completed in 2 days. Find the
number of days required for each of them to do the work completely.
Solve any four of the following.
If x is the geometric mean of 16 and 9, find x.
Find the sum of all numbers from 50 to 350 which are divisible by 4. Also, find the 15th term.
Find tn for the A.P. 3,8,13,18,.....
If for an A.P. the first term is 2 and the common difference is 3, then find first three-term of A.P.
