Advertisements
Advertisements
Question
Which radioactive isotope would have the longer half-life 15O or 19O? (Given rate constants for 15O and 19O are 5.63 × 10–3 s–1 and k = 2.38 × 10–2 s–1 respectively.)
Options
15O
19O
Both will have the same half-life
None of the above, information given is insufficient
Solution
15O
Explanation:
The rate constant for the decay of 15O is less than that for 19O. Therefore, the rate of decay of 15O will be slower and will have a longer half-life.
APPEARS IN
RELATED QUESTIONS
Sucrose decomposes in acid solution to give glucose and fructose according to the first order rate law. The half life of the reaction is 3 hours. Calculate fraction of sucrose which will remain after 8 hours.
The rate constant for the first order decomposition of H2O2 is given by the following equation:
log k = 14.34 − 1.25 × 104 K/T. Calculate Ea for this reaction and at what temperature will its half-period be 256 minutes?
The half-life period of zero order reaction A → product is given by
(a) `([A]_0)/k`
(b) `0.693/k`
(c) `[A]_0/(2k)`
(d) `(2[A]_0)/k`
Show that for a first order reaction half life is independent of initial concentration.
The rate constant for a first order reaction is 1.54 × 10−3 s−1. Calculate its half life time.
Read the passage given below and answer the following question.
|
Are there nuclear reactions going on in our bodies? There are nuclear reactions constantly occurring in our bodies, but there are very few of them compared to the chemical reactions, and they do not affect our bodies much. All of the physical processes that take place to keep a human body running are chemical processes. Nuclear reactions can lead to chemical damage, which the body may notice and try to fix. The nuclear reaction occurring in our bodies is radioactive decay. This is the change of a less stable nucleus to a more stable nucleus. Every atom has either a stable nucleus or an unstable nucleus, depending on how big it is and on the ratio of protons to neutrons. The ratio of neutrons to protons in a stable nucleus is thus around 1 : 1 for small nuclei (Z < 20). Nuclei with too many neutrons, too few neutrons, or that are simply too big are unstable. They eventually transform to a stable form through radioactive decay. Wherever there are atoms with unstable nuclei (radioactive atoms), there are nuclear reactions occurring naturally. The interesting thing is that there are small amounts of radioactive atoms everywhere: in your chair, in the ground, in the food you eat, and yes, in your body. The most common natural radioactive isotopes in humans are carbon-14 and potassium-40. Chemically, these isotopes behave exactly like stable carbon and potassium. For this reason, the body uses carbon-14 and potassium-40 just like it does normal carbon and potassium; building them into the different parts of the cells, without knowing that they are radioactive. In time, carbon-14 atoms decay to stable nitrogen atoms and potassium-40 atoms decay to stable calcium atoms. Chemicals in the body that relied on having a carbon-14 atom or potassium-40 atom in a certain spot will suddenly have a nitrogen or calcium atom. Such a change damages the chemical. Normally, such changes are so rare, that the body can repair the damage or filter away the damaged chemicals. The natural occurrence of carbon-14 decay in the body is the core principle behind carbon dating. As long as a person is alive and still eating, every carbon-14 atom that decays into a nitrogen atom is replaced on average with a new carbon-14 atom. But once a person dies, he stops replacing the decaying carbon-14 atoms. Slowly the carbon-14 atoms decay to nitrogen without being replaced, so that there is less and less carbon-14 in a dead body. The rate at which carbon-14 decays is constant and follows first order kinetics. It has a half-life of nearly 6000 years, so by measuring the relative amount of carbon-14 in a bone, archeologists can calculate when the person died. All living organisms consume carbon, so carbon dating can be used to date any living organism, and any object made from a living organism. Bones, wood, leather, and even paper can be accurately dated, as long as they first existed within the last 60,000 years. This is all because of the fact that nuclear reactions naturally occur in living organisms. |
Suppose an organism has 20 g of Carbon-14 at its time of death. Approximately how much Carbon-14 remains after 10,320 years? (Given antilog 0.517 = 3.289)
Observe the graph shown in figure and answer the following questions:
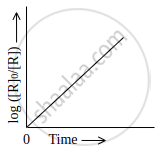
Write the relationship between k and t1/2 (half-life period)
A sample of U238 (half-life = 4.5 × 109 years) ore is found to contain 23.8 g of U238 and 20.6 g of Pb206. The age of the ore is ______ × 109 years.
The rate of a first order reaction is 0.04 mol litre-1 s-1 at 10 minutes and 0.03 mol litre-1 sec-1 at 20 minutes after initiation. The half-life of the reaction is ______ min.
Obtain a relation, `k_2/k_1 = ((t_(1/2))_2)/((t_(1/2))_1)`, where k1 and k2 are rate constants while (t1/2)1 and (t1/2)2 are half-life periods of the first order reaction at temperatures T1 and T2 respectively. Write the relation for activation energy.
